题目内容
已知f(2x+1)=4x+
,则f(x)= .
| 3 |
| 2 |
考点:函数的值
专题:函数的性质及应用
分析:设2x+1=t,则x=
,由此能求出结果.
| t-1 |
| 2 |
解答:
解:∵知f(2x+1)=4x+
,
设2x+1=t,则x=
,
∴f(t)=2(t-1)+
=2t-
,
∴f(x)=2x-
.
故答案为:2x-
.
| 3 |
| 2 |
设2x+1=t,则x=
| t-1 |
| 2 |
∴f(t)=2(t-1)+
| 3 |
| 2 |
| 1 |
| 2 |
∴f(x)=2x-
| 1 |
| 2 |
故答案为:2x-
| 1 |
| 2 |
点评:本题考查函数值的求法,解题时要认真审题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
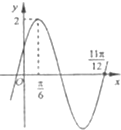 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[-
| π |
| 2 |
正三棱柱ABC-A1B1C1的底面边长为3,侧棱AA1=
,D是CB延长线上一点,且BD=BC,则二面角B1-AD-B的大小( )
| 3 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|