题目内容
2.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=m-\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$(其中t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρ=2(1)若直线l与曲线C有且只有一个公共点,求m的值;
(2)若点P(m,0),直线l与曲线C交于相异两点A,B,求|PA|•|PB|的取值范围.
分析 (1)将直线l的参数方程代入曲线C的普通方程,令判别式等于0解出m;
(2)令判别式大于0解出m的取值范围,利用关于系数的关系得出|PA|•|PB|关于m的函数,根据m的范围解出.
解答 解:(1)曲线C的直角坐标方程为x2+y2=4,
将直线l的参数方程代入上式得:t2-$\sqrt{2}m$t+m2-4=0,
∵直线l与曲线C有且只有一个公共点,
∴(-$\sqrt{2}$m)2-4(m2-4)=0,解得m=$±2\sqrt{2}$.
(2)∵直线l与曲线C交于相异两点A,B,
∴(-$\sqrt{2}$m)2-4(m2-4)>0,解得-2$\sqrt{2}$<m<2$\sqrt{2}$.
设A,B对应的参数分别为t1,t2,则t1t2=m2-4.
∴|PA|•|PB|=|t1t2|=|m2-4|.
∵-2$\sqrt{2}$<m<2$\sqrt{2}$,∴0<m2<8,∴0≤|m2-4|<4.
∴|PA|•|PB|的取值范围是[0,4).
点评 本题考查了极坐标方程与直角坐标方程的转化,直线参数方程的几何意义与应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,则( )
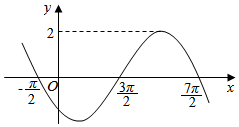

| A. | A=2,ω=2,φ=$\frac{3π}{4}$ | B. | A=2,ω=2,φ=$\frac{5π}{4}$ | C. | A=2,ω=$\frac{1}{2}$,φ=$\frac{3π}{4}$ | D. | A=2,ω=$\frac{1}{2}$,φ=$\frac{5π}{4}$ |
7.已知x,y满足约束条件$\left\{\begin{array}{l}x-y+5≥0\\ x≤2\\ x+y≥0\end{array}\right.$,则z=x+2y的最小值为( )
| A. | -3 | B. | $-\frac{5}{2}$ | C. | -2 | D. | $\frac{5}{2}$ |
 如图,点D是△ABC的边BC上一点,且AC=$\sqrt{3}$AD,$\sqrt{3}$CD=2AC,CD=2BD.
如图,点D是△ABC的边BC上一点,且AC=$\sqrt{3}$AD,$\sqrt{3}$CD=2AC,CD=2BD.