题目内容
20．
如图，平面ABCD⊥平面ABEF，四边形ABCD是矩形，四边形ABEF是等腰梯形，其中AB∥EF，AB=2AF，∠BAF=60°，O，P分别为AB，CB的中点，M为△OBF的重心．（I）求证：平面ADF⊥平面CBF；
（II）求证：PM∥平面AFC．
分析 （I）利用面面垂直的性质可证CB⊥平面ABEF，利用线面垂直的性质可证CB⊥AF，设AF=a，则AB=2a，根据余弦定理可得BF=$\sqrt{3}a$，利用勾股定理可得AF⊥BF，从而可证AF⊥平面CBF，进而可证平面ADF⊥平面CBF．
（II）∵M为底面△OBF的重心，连接OM延长交BF于Q，则Q为BF的中点，连接PO，PQ，可得PO∥AC，PQ∥CF，从而可证PO∥平面AFC，PQ∥平面AFC，通过面面平行即可证明PM∥平面AFC．
解答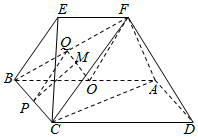 
（本题满分为12分）
证明：（I）∵平面ABCD⊥平面ABEF，且CB⊥AB，
∴CB⊥平面ABEF，…2分
又∵AF?平面ABEF，
∴CB⊥AF，…3分
∵AB=2AF，设AF=a，则AB=2a，又∠BAF=60°，根据余弦定理BF=$\sqrt{3}a$，
∴AB2=AF2+BF2，从而AF⊥BF，
∴AF⊥平面CBF，…4分
又∵AF?平面ADF，
∴平面ADF⊥平面CBF．…6分
（II）∵M为底面△OBF的重心，连接OM延长交BF于Q，则Q为BF的中点，连接PO，PQ，
∵P，O，Q分别是CB，AB，BF的中点，
∴PO∥AC，PQ∥CF，
从而，PO∥平面AFC，PQ∥平面AFC，…8分
∴平面POQ∥平面AFC，…10分
又∵PM?平面POQ，
∴PM∥平面AFC．…12分
点评 本题主要考查了面面垂直、线面垂直的性质，线面垂直、面面垂直的判定，线面平行的判定，考查了余弦定理，勾股定理的应用，考查了空间想象能力和推理论证能力，属于中档题．
练习册系列答案
相关题目
10．函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜2π）一个周期的图象如图所示，则（ ）
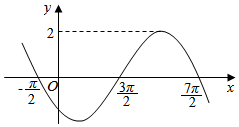
| A． | A=2，ω=2，φ=$\frac{3π}{4}$ | B． | A=2，ω=2，φ=$\frac{5π}{4}$ | C． | A=2，ω=$\frac{1}{2}$，φ=$\frac{3π}{4}$ | D． | A=2，ω=$\frac{1}{2}$，φ=$\frac{5π}{4}$ |
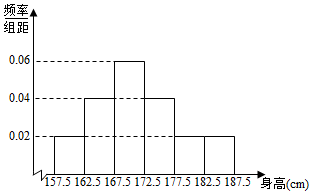某省高中男生身高统计调查数据显示：全省100000名男生的身高服从正态分布N（170.5，16）．现从某学校高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于157.5cm和187.5cm之间，将测量结果按如下方式分成6组：第1组[157.5，162.5），第2组[162.5，167.5），…，第6组[182.5，187.5]，如图是按上述分组方法得到的频率分布直方图．
15．过抛物线y2=4x的焦点F作直线l，与抛物线分别交于A、B两点（A点在第一象限），若S△AOB=3S△FOB，则直线l的斜率k=（ ）
| A． | $\sqrt{3}$ | B． | 2 | C． | 2$\sqrt{2}$ | D． | 3 |