题目内容
17.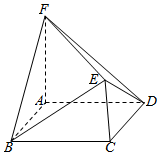 如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.
如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.(1)求证:EF⊥平面BED;
(2)当三棱锥E-BDF的体积为4时,求多面体EF-ABCD的表面积.
分析 (1)连接AC,BD,可得AC⊥BD,再由AF⊥底面ABCD,得到平面ACEF⊥平面ABCD,结合面面垂直的性质得BD⊥平面ACEF,则BD⊥EF,设CE=a,得AB=a,AF=2a,通过求解直角三角形得$O{E}^{2}={a}^{2}+(\frac{\sqrt{2}}{2}a)^{2}=\frac{3}{2}{a}^{2}$,$O{F}^{2}=4{a}^{2}+(\frac{\sqrt{2}}{2}a)^{2}=\frac{9}{2}{a}^{2}$,$E{F}^{2}={a}^{2}+(\sqrt{2}a)^{2}=3{a}^{2}$,由勾股定理可得EF⊥OE,由线面垂直的判定EF⊥平面BED;
(2)由三棱锥E-BDF的体积为4,结合等积法得三棱锥F-BDE的体积为4,代入三棱锥体积公式求得a值,则多面体EF-ABCD的表面积可求.
解答 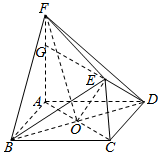 (1)证明:如图,
(1)证明:如图,
连接AC,BD,
∵四边形ABCD为正方形,
∴AC⊥BD,
设AC∩BD=O,连接AO,EO,
∵AF⊥底面ABCD,AF?平面ACEF,
∴平面ACEF⊥平面ABCD,
又平面ACEF∩平面ABCD,
∴BD⊥平面ACEF,则BD⊥EF,
设CE=a,由AF=2AB=2CE,得AB=a,AF=2a,
∴AO=OC=$\frac{\sqrt{2}}{2}a$,
则$O{E}^{2}={a}^{2}+(\frac{\sqrt{2}}{2}a)^{2}=\frac{3}{2}{a}^{2}$,$O{F}^{2}=4{a}^{2}+(\frac{\sqrt{2}}{2}a)^{2}=\frac{9}{2}{a}^{2}$,
过E作EG⊥AF于G,则$E{F}^{2}={a}^{2}+(\sqrt{2}a)^{2}=3{a}^{2}$,
∵EF2+OE2=OF2,
∴EF⊥OE,又OE∩BD=O,
∴EF⊥平面BED;
(2)三棱锥E-BDF的体积为4,即三棱锥F-BDE的体积为4,
∴${V}_{F-BED}=\frac{1}{3}×\frac{1}{2}×\sqrt{2}a×\frac{\sqrt{6}}{2}a×\sqrt{3}a=4$,
解得:a=2.
∴多面体EF-ABCD的表面积为S=2×2+2×$\frac{1}{2}×2×2$+2×$\frac{1}{2}×2×4$+2×$\frac{1}{2}×2\sqrt{2}×12$=$16+24\sqrt{2}$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了等积法求三棱锥的体积,是中档题.

| A. | -3 | B. | $-\frac{5}{2}$ | C. | -2 | D. | $\frac{5}{2}$ |
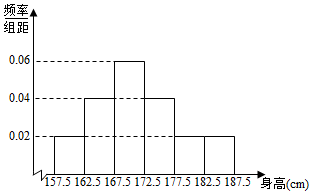 某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.
某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图.