题目内容
已知数列{an}的前项和Sn=n2+2n.
(1)求证:{an}是等差数列;
(2)设bn=an•2n-1,求数列{bn}的前n项和Tn;
(3)在(2)的条件下,求证:数列{bn}中任何三项都不可能成等比数列.
(1)求证:{an}是等差数列;
(2)设bn=an•2n-1,求数列{bn}的前n项和Tn;
(3)在(2)的条件下,求证:数列{bn}中任何三项都不可能成等比数列.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)当n≥2时,an=Sn-Sn-1=2n+1,a1=S1=3符合上式,由此得到an=2n+1,n∈N*,从而能证明数列{an}是等差数列.
(2)由bn=(2n+1)•2n-1,利用错位相减法能求出数列{bn}的前n项和Tn.
(3)假设数列{an}中存在三项as,at,ak(s,t,k∈N*,且s<t<k)成等比数列,利用反证法能推导出这个假设不成立,从而证明数列{bn}中任何三项都不可能成等比数列.
(2)由bn=(2n+1)•2n-1,利用错位相减法能求出数列{bn}的前n项和Tn.
(3)假设数列{an}中存在三项as,at,ak(s,t,k∈N*,且s<t<k)成等比数列,利用反证法能推导出这个假设不成立,从而证明数列{bn}中任何三项都不可能成等比数列.
解答:
(1)证明:当n≥2时,an=Sn-Sn-1
=(n2+2n)-[(n-1)2+2(n-1)]=2n+1,
a1=S1=3符合上式,
∴an=2n+1,n∈N*,
∵an+1-an=[2(n+1)-1]-(2n+1)=2,
∴数列{an}是等差数列.
(2)解:∵bn=(2n+1)•2n-1,
∴Tn=3•20+5•2+7•22+…+(2n+1)•2n-1,
2Tn=3•2+5•22+7•23+…+(2n+1)•2n,
两式相减,得:
-Tn=3•20+2(2+22+23+…+2n-1)-(2n+1)•2n
=3+2×
-(2n+1)•2n,
∴Tn=(2n-1)•2n+1.
(3)证明:假设数列{an}中存在三项as,at,ak(s,t,k∈N*,且s<t<k)成等比数列,
则[(2s+1)•2s-1]•[(2k+1)•2k-1]=[(2t+1)•2t-1]2,
∴(2s+1)(2k+1)•2s+k=(2t+1)•22t.
①若s+k=2t,则(2s+1)(2k+1)=(2t+1)2,
∴4sk+2(s+k)+1=4t2+4t+1,
∴sk=
(s+k)2,∴s=k,与s<k矛盾.
②若s+k>2t,则(2s+1)(2k+1)•2s+k-2t=(2t+1)2,
上式左边是偶数,右边是奇数,矛盾.
③若s+k<2t,则(2s+1)(2k+1)=(2t+1)2•22t-(s+k),
上式左边是奇数,右边是偶数,矛盾.
综上所述,数列{bn}中任何三项都不可能成等比数列.
=(n2+2n)-[(n-1)2+2(n-1)]=2n+1,
a1=S1=3符合上式,
∴an=2n+1,n∈N*,
∵an+1-an=[2(n+1)-1]-(2n+1)=2,
∴数列{an}是等差数列.
(2)解:∵bn=(2n+1)•2n-1,
∴Tn=3•20+5•2+7•22+…+(2n+1)•2n-1,
2Tn=3•2+5•22+7•23+…+(2n+1)•2n,
两式相减,得:
-Tn=3•20+2(2+22+23+…+2n-1)-(2n+1)•2n
=3+2×
| 2(1-2n-1) |
| 1-2 |
∴Tn=(2n-1)•2n+1.
(3)证明:假设数列{an}中存在三项as,at,ak(s,t,k∈N*,且s<t<k)成等比数列,
则[(2s+1)•2s-1]•[(2k+1)•2k-1]=[(2t+1)•2t-1]2,
∴(2s+1)(2k+1)•2s+k=(2t+1)•22t.
①若s+k=2t,则(2s+1)(2k+1)=(2t+1)2,
∴4sk+2(s+k)+1=4t2+4t+1,
∴sk=
| 1 |
| 4 |
②若s+k>2t,则(2s+1)(2k+1)•2s+k-2t=(2t+1)2,
上式左边是偶数,右边是奇数,矛盾.
③若s+k<2t,则(2s+1)(2k+1)=(2t+1)2•22t-(s+k),
上式左边是奇数,右边是偶数,矛盾.
综上所述,数列{bn}中任何三项都不可能成等比数列.
点评:本题考查等差数列的证明,考查数列的通项公式的求法,考查数列{bn}中任何三项都不可能成等比数列的证明.解题时要注意反证法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
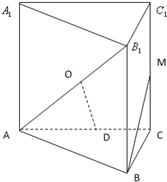 已知直三棱柱ABC-A1B1C1的底面△ABC中,∠C=90°,BC=
已知直三棱柱ABC-A1B1C1的底面△ABC中,∠C=90°,BC=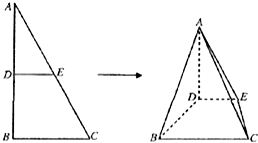 如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.
如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED. 如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.
如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.