题目内容
已知数列{bn}前n项和Sn=
n2-
n.数列{an}满足
=4-(bn+2)(n∈N*),数列{cn}满足cn=anbn.
(1)求数列{an}和数列{bn}的通项公式;
(2)求数列{cn}的前n项和Tn;
(3)若cn≤
m2+m-1对一切正整数n恒成立,求实数m的取值范围.
| 3 |
| 2 |
| 1 |
| 2 |
| a | 3 n |
(1)求数列{an}和数列{bn}的通项公式;
(2)求数列{cn}的前n项和Tn;
(3)若cn≤
| 1 |
| 4 |
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)利用Sn=
n2-
n,再写一式,两式相减,即可求得通项bn,进而求得通项an.
(2)先求得cn,进而利用错位相减法即可求得Tn.
(3)求出cn的最大值,即可求实数m的取值范围.
| 3 |
| 2 |
| 1 |
| 2 |
(2)先求得cn,进而利用错位相减法即可求得Tn.
(3)求出cn的最大值,即可求实数m的取值范围.
解答:
解:(1)由已知和得,当n≥2时,bn=Sn-Sn-1=(
n2-
n)-(
(n-1)2-
(n-1))=3n-2
又b1=1=3×1-2,符合上式.故数列{bn}的通项公式bn=3n-2.
又∵
=4-(bn+2),∴an=4-
=4-
=(
)n,
故数列{an}的通项公式为an=(
)n,
(2)cn=anbn=(3n-2)•(
)n,
∴Sn=1×
+4×(
)2+7×(
)3+…+(3n-2)×(
)n,
Sn=1×(
)2+4×(
)3+7×(
)4+…+(3n-5)×(
)n+(3n-2)×(
)n+1,
①-②得
Sn=
+3×[(
)2+(
)3+(
)4+…+(
)n]-(3n-2)×(
)n+1
=
+3×
-(3n-2)×(
)n+1=
-(3n+2)×(
)n+1,
∴Sn=
-
×(
)n+1═
-
×(
)n.
(3)∵cn=(3n-2)•(
)n,
∴cn+1-cn=(3n+1)•(
)n+1-(3n-2)•(
)n=(
)n•[
-(3n-2)]=-9•(
)n+1(n-1),
当n=1时,cn+1=cn;当n≥2时,cn+1≤cn,
∴(cn)max=c1=c2=
.
若cn≤
m2+m-1对一切正整数n恒成立,
则
m2+m-1≥
即可,解得m≤-5或m≥1.
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
又b1=1=3×1-2,符合上式.故数列{bn}的通项公式bn=3n-2.
又∵
| a | 3 n |
| (bn+2) |
| 3 |
| (3n-2)+2 |
| 3 |
| 1 |
| 4 |
故数列{an}的通项公式为an=(
| 1 |
| 4 |
(2)cn=anbn=(3n-2)•(
| 1 |
| 4 |
∴Sn=1×
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
①-②得
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
(
| ||||
1-
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴Sn=
| 2 |
| 3 |
| 12n+8 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3n+2 |
| 3 |
| 1 |
| 4 |
(3)∵cn=(3n-2)•(
| 1 |
| 4 |
∴cn+1-cn=(3n+1)•(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3n+1 |
| 4 |
| 1 |
| 4 |
当n=1时,cn+1=cn;当n≥2时,cn+1≤cn,
∴(cn)max=c1=c2=
| 1 |
| 4 |
若cn≤
| 1 |
| 4 |
则
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查了已知数列的前n项和求通项及利用错位相减法求数列的前n项和,考查恒成立问题,掌握方法是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
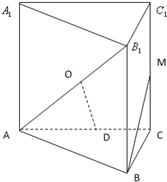 已知直三棱柱ABC-A1B1C1的底面△ABC中,∠C=90°,BC=
已知直三棱柱ABC-A1B1C1的底面△ABC中,∠C=90°,BC= 如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.
如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.