题目内容
函数y=x3+x2+mx+1在实数集上是单调函数，则m的取值范围是 ．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求函数的导数，根据函数的单调性和导数之间的关系，即可得到结论．
解答：
解：函数的导数为y′=f′（x）=3x2+2x+m，
∵f′（x）=3x2+2x+m是抛物线，开口向上，
∴要使函数y=x3+x2+mx+1在实数集上是单调函数，
若函数为单调递减，则f′（x）=3x2+2x+m≤0恒成立，此时不可能．
若函数为单调递增，则f′（x）=3x2+2x+m≥0恒成立，此时判别式△=4-4×3m≤0，
即m≥
．
故答案为：m≥
．
∵f′（x）=3x2+2x+m是抛物线，开口向上，
∴要使函数y=x3+x2+mx+1在实数集上是单调函数，
若函数为单调递减，则f′（x）=3x2+2x+m≤0恒成立，此时不可能．
若函数为单调递增，则f′（x）=3x2+2x+m≥0恒成立，此时判别式△=4-4×3m≤0，
即m≥
| 1 |
| 3 |
故答案为：m≥
| 1 |
| 3 |
点评：本题主要考查函数单调性和导数之间的关系，利用导数恒成立结合二次函数的性质是解决本题的关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
直线y=x+
被曲线y=
x2截得线段的中点到原点的距离为（ ）
| 3 |
| 2 |
| 1 |
| 2 |
| A、29 | ||||
B、
| ||||
C、
| ||||
D、
|
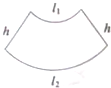如图是一个扇环（圆环的一部分），两段圆弧的长分别为l1，l2，另外两边的长为h，先把这个扇环与梯形类比，然后根据梯形的面积公式写出这个扇环的面积并证明其正确性．参考公式：
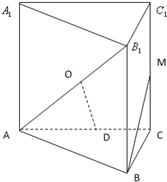已知直三棱柱ABC-A1B1C1的底面△ABC中，∠C=90°，BC=
如图，已知，圆O内接四边形BEGD，AB切圆O于点B，且与四边形BEGD对角线ED延长线交于点A，CD切圆O于点D，且与EG延长线交于点C；延长BD交AC于点Q，若AB=AC．