题目内容
等差数列{an}中,已知d>0且a2•a3=15,a1+a4=8.
(1)求{an}的通项公式
(2)bn=
数列{bn}的前n项和Sn,求证:Sn<
.
(1)求{an}的通项公式
(2)bn=
| 1 |
| an•an+1 |
| 1 |
| 2 |
考点:数列与不等式的综合,等差数列的前n项和
专题:综合题,等差数列与等比数列
分析:(1)利用等差数列的性质,求出首项羽公差,即可求{an}的通项公式;
(2)利用裂项法求和,即可证明结论.
(2)利用裂项法求和,即可证明结论.
解答:
(1)解:∵{an}是等差数列,∴a1+a4=a2+a3=8(1分)
又∵a2•a3=15且d>0,
∴a2=3,a3=5(4分)
∴d=2,a1=a2-d=1(5分)
∴an=a1+(n-1)d=2n-1(n∈N+)(6分)
(2)证明:bn=
=
=
(
-
)(9分)
∴Sn=b1+b2+…+bn=
(1-
+
-
+…+
-
)(11分)
=
(1-
)<
(12分)
又∵a2•a3=15且d>0,
∴a2=3,a3=5(4分)
∴d=2,a1=a2-d=1(5分)
∴an=a1+(n-1)d=2n-1(n∈N+)(6分)
(2)证明:bn=
| 1 |
| an•an+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Sn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
点评:本题考查数列的通项羽求和,考查裂项法,考查学生分析解决问题的能力,确定数列的通项是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
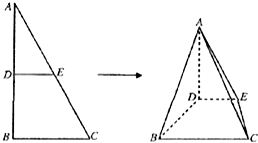 如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.
如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED. 如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.
如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.