题目内容

设点M是线段BC的中点，点A在直线BC外，|
BC
|=4，|
AB
+
AC
|=|
AB
-
AC
|，则
AM
•(
AB
+
AC
)=（　　）
A、8B、4C、2D、1
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量的中点表示，可得
AM
•(
AB
+
AC
)=2
AM
2，再由向量的平方即为模的平方，可得AB⊥AC，结合直角三角形的斜边的中线即为斜边的一半，即可计算得到．
解答： 解：点M是线段BC的中点，
则有
AM
=
1
2
（
AB
+
AC
），
即有
AB
+
AC
=2
AM
，
则
AM
•(
AB
+
AC
)=2
AM
2，
由于|
AB
+
AC
|=|
AB
-
AC
|，
即（
AB
+
AC
）2=（
AB
-
AC
）2，
AB
2+
AC
2+2
AB
•
AC
=
AB
2+
AC
2-2
AB
•
AC
，
即有
AB
•
AC
=0，
即有AB⊥AC，
由于M为BC的中点，|
BC
|=4，
则|
AM
|=
1
2
|
BC
|=2，
则
AM
•(
AB
+
AC
)=2
AM
2=2×22=8．
故选A．
点评：本题考查向量的数量积的性质和中点的向量表示，同时考查向量垂直的条件，运用直角三角形的斜边的中线即为斜边的一半是解题的关键．
练习册系列答案
相关题目
如图，直四棱柱ABCD-A1B1C1D1的底面是菱形，侧面是正方形，∠DAB=60°，E是棱CB的延长线上一点，经过点A、C1、E的平面交棱BB1于点F，B1F=2BF．
（1）求证：平面AC1E⊥平面BCC1B1；
（2）求二面角E-AC1-C的平面角的余弦值．
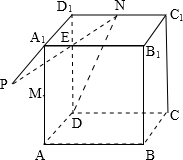如图，在一封闭的正方体容器内装满水，M、N分别是AA1与C1D1的中点，由于某种原因，在D、M、N三点处各有一个小洞，为此容器内存水最多，问应将此容器如何放置？此时水的上表面的形状怎样？
设a是一个平面，Γ是平面α上的一个图形，若在平面α上存在一个定点A和一个定角θ（θ∈（0，2π），使得Γ上的任意一点以A为中心顺时针（或逆时针）旋转角θ，所得到的图形与原图形Γ重合，则称点A为对称中心，θ为旋转角，Γ为旋转对称图形，若以下4个图形，从左至右依次是正三角形、正方形、正五边形、正六边形，它们都是旋转对称图形，则它们的最小旋转角依次为
 
，若Γ是一个正n边形，则其最小旋转角n可以表示为
 
．
设
e1
，
e2
是两个不共线的向量，已知向量
AB
=2
e1
+tanα•
e2
，
CB
=
e1
-
5
4
e2
，
CD
=2
e1
-
e2
，若A，B，D三点共线，则
2sinα-cosα
sinα+cosα
=
 
．
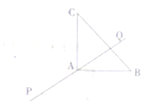如图，在Rt△ABC中，|
PA
|=|
BC
|=a且
PA
=
1
2
PQ
，向
PQ
和
BC
的夹角θ取何值，
CP
•
BQ
的值最大？并求出这个最大值．
如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（　　）
A、（2+
5
）π
B、4π
C、（2+2
2
）π
D、6π
已知单位向量
e1
、
e2
的夹角为60°，则|2
e1
+3
e2
|=
 
．
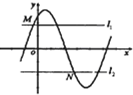如图：M（xM，yM），N（xN，yN）分别是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与两条直线l1：y=m，l2：y=-m（A≥m≥0）的两个交点，记S=|xN-xM|，则S（m）图象大致是（　　）
A、
B、
C、
D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网