题目内容
设a是一个平面,Γ是平面α上的一个图形,若在平面α上存在一个定点A和一个定角θ(θ∈(0,2π),使得Γ上的任意一点以A为中心顺时针(或逆时针)旋转角θ,所得到的图形与原图形Γ重合,则称点A为对称中心,θ为旋转角,Γ为旋转对称图形,若以下4个图形,从左至右依次是正三角形、正方形、正五边形、正六边形,它们都是旋转对称图形,则它们的最小旋转角依次为 ,若Γ是一个正n边形,则其最小旋转角n可以表示为 .


考点:归纳推理
专题:综合题,推理和证明
分析:由题意,对称中心为正多边形的中心,正三角形、正方形、正五边形、正六边形,它们都是旋转对称图形,则它们的最小旋转角依次为
,
=
,
,
=
;由此可得Γ是一个正n边形的最小旋转角.
| 2π |
| 3 |
| 2π |
| 4 |
| π |
| 2 |
| 2π |
| 5 |
| 2π |
| 6 |
| π |
| 3 |
解答:
解:由题意,对称中心为正多边形的中心,正三角形、正方形、正五边形、正六边形,它们都是旋转对称图形,则它们的最小旋转角依次为
,
=
,
,
=
;Γ是一个正n边形,则其最小旋转角n可以表示为
.
故答案为:
,
,
,
;
.
| 2π |
| 3 |
| 2π |
| 4 |
| π |
| 2 |
| 2π |
| 5 |
| 2π |
| 6 |
| π |
| 3 |
| 2π |
| n |
故答案为:
| 2π |
| 3 |
| π |
| 2 |
| 2π |
| 5 |
| π |
| 3 |
| 2π |
| n |
点评:所谓归纳推理,就是从个别性知识推出一般性结论的推理.它与演绎推理的思维进程不同.归纳推理的思维进程是从个别到一般,而演绎推理的思维进程不是从个别到一般,是一个必然地得出的思维进程.

练习册系列答案
相关题目
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A、100 cm3 |
| B、108 cm3 |
| C、84 cm3 |
| D、92 cm3 |
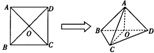 已知正方形ABCD的边长为1,AC∩BD=O,将正方形ABCD沿对角线折起,使AC=1,得到三棱锥A-BCD,如图所示.
已知正方形ABCD的边长为1,AC∩BD=O,将正方形ABCD沿对角线折起,使AC=1,得到三棱锥A-BCD,如图所示.
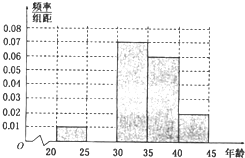 在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,据此估计这800名志愿者年龄在[25,30)的人数为
在某市“创建文明城市”活动中,对800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,据此估计这800名志愿者年龄在[25,30)的人数为