题目内容
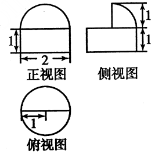
如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）
A、（2+
| ||
| B、4π | ||
C、（2+2
| ||
| D、6π |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知的三视图可得：该几何体是一个半球与一个圆锥组合而成的几何体，分别计算出两个曲面的面积，可得答案．
解答：
解：由已知的三视图可得：该几何体是一个半球与一个圆锥组合而成的几何体，
半球的半径为1，故半球面面积为：2π，
圆锥的底面半径为1，高为2，故母线长为
，
故圆锥的侧面积为：
π，
故组合体的表面积是：（2+
）π，
故选：A
半球的半径为1，故半球面面积为：2π，
圆锥的底面半径为1，高为2，故母线长为
| 5 |
故圆锥的侧面积为：
| 5 |
故组合体的表面积是：（2+
| 5 |
故选：A
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
若
，
是两个非零向量，且|
|=|
|=λ|
+
|，λ∈[
，1]，则
与
-
的夹角的取值范围是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| ||
| 3 |
| b |
| a |
| b |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
一个几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若双曲线C：
-
=1的一条渐近线的倾斜角为
，则双曲线C的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、2或
| ||||
B、
| ||||
C、2或
| ||||
| D、2 |