题目内容

19．若实数x，y满足约束条件$\left\{\begin{array}{l}{x≤2}\\{y≤x}\\{x+y≥1}\end{array}\right.$，则z=3x+y的最大值为（　　）
A．1B．2C．5D．8

分析 作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z的最大值．

解答 解：作出不等式对应的平面区域如图，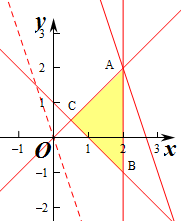
由z=3x+y，得y=-3x+z，
平移直线y=-3x+z，由图象可知当直线y=-3x+z，经过点A时，直线y=-3x+z的截距最大，
此时z最大．
由$\left\{\begin{array}{l}{x=2}\\{y=x}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$，即A（2，2）
此时z的最大值为，zmax=3×2+2=8．
故选：D．

点评 本题主要考查线性规划的应用，根据z的几何意义，利用数形结合是解决本题的关键．

练习册系列答案
相关题目
9．已知△ABC在正方形网格中的位置如图所示，则cos∠ABC=（　　）
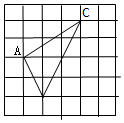
A．$\frac{3}{10}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$
10．观察下列各式：55=3125，56=15625，57=78125，…，则52017的末四位数字为（　　）
A．3125B．5625C．0625D．8125
7．已知f（x）=x3+3x-1，f（a-3）=-3，f（b-3）=1，则a+b的值为6．
14．在y=sin|x|，y=|sinx|，y=sin（2x+$\frac{2π}{3}$），y=cos（$\frac{x}{2}$+$\frac{2π}{3}$），y=cosx+|cosx|$y=tan\frac{1}{2}x+1$中，最小正周期为π的函数的个数是（　　）
A．1个B．2个C．3个D．4个
4．长方体ABCD-A1B1C1D1中，$DC+C{C_1}=8，CB=4，\overrightarrow{AM}=\overrightarrow{MB}$，点N是平面A1B1C1D1上的点，且满足${C_1}N=\sqrt{5}$，当长方体ABCD-A1B1C1D1的体积最大时，线段MN的最小值是（　　）
A．$6\sqrt{2}$B．8C．$\sqrt{21}$D．$4\sqrt{3}$
11．已知集合A={2，4，6，8}，B={x|3≤x≤6}，则A∩B=（　　）
A．{2，4}B．{4，6}C．{6，8}D．{3，4，6}
8．化直线l的参数方程$\left\{\begin{array}{l}{x=-3+t}\\{y=1+\sqrt{3}t}\end{array}\right.$，（t为参数）为普通方程，并求倾斜角．
9．某几何体的三视图如图所示（单位：cm），则该几何体的侧面PAB的面积是（　　）
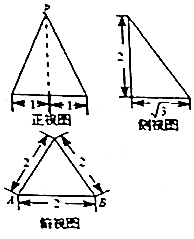
A．$\sqrt{7}$B．2C．1D．$\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网