题目内容
14.在y=sin|x|,y=|sinx|,y=sin(2x+$\frac{2π}{3}$),y=cos($\frac{x}{2}$+$\frac{2π}{3}$),y=cosx+|cosx|$y=tan\frac{1}{2}x+1$中,最小正周期为π的函数的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别求出各个函数的最小正周期,判断即可
解答 解:y=sin|x|不是周期函数,
y=|sinx|的最小正周期为π,
y=sin(2x+$\frac{2π}{3}$)最小正周期为π,
y=cos($\frac{x}{2}$+$\frac{2π}{3}$)最小正周期为4π
y=cosx+|cosx|最小正周期为2π,
$y=tan\frac{1}{2}x+1$最小正周期为2π,
故最小正周期为π的函数的个数是2个,
故选:B
点评 本题考查三角函数的周期性及其求法,着重考查三角函数的周期的确定,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
4.函数$f(x)=\sqrt{x-1}+lg({x+1})$的定义域是( )
| A. | (-1,1] | B. | (-1,1) | C. | [-1,1] | D. | [1,+∞) |
5.定积分${∫}_{0}^{1}$(x+sinx)dx的值为( )
| A. | $\frac{3}{2}$-cos1 | B. | $\frac{{π}^{2}}{2}$+1 | C. | π | D. | $\frac{1}{2}$ |
19.若实数x,y满足约束条件$\left\{\begin{array}{l}{x≤2}\\{y≤x}\\{x+y≥1}\end{array}\right.$,则z=3x+y的最大值为( )
| A. | 1 | B. | 2 | C. | 5 | D. | 8 |
6.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
3.在极坐标系中,点M(1,0)关于极点的对称点为( )
| A. | (1,0) | B. | (-1,π) | C. | (1,π) | D. | (1,2π) |
4.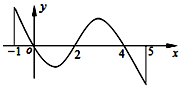 已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.
已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.
下列关于函数f(x)的命题:
①函数f(x)的极大值点有2个;
②函数f(x)在[0,2]上是减函数;
③若x∈[-1,t]时,f(x)的最大值是2,则t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中是真命题的是①②.(填写序号)
 已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.
已知函数f(x)定义域为[-1,5],部分对应值如表,f(x)的导函数f′(x)的图象如图所示.| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
①函数f(x)的极大值点有2个;
②函数f(x)在[0,2]上是减函数;
③若x∈[-1,t]时,f(x)的最大值是2,则t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中是真命题的是①②.(填写序号)
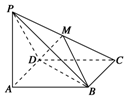 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).
如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,请你补充一个条件①(或③),使平面MBD⊥平面PCD.①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC(填写你认为是正确的条件对应的序号).