题目内容
9．某几何体的三视图如图所示（单位：cm），则该几何体的侧面PAB的面积是（ ）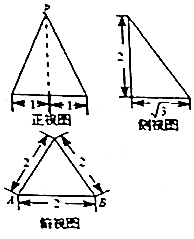
| A． | $\sqrt{7}$ | B． | 2 | C． | 1 | D． | $\sqrt{3}$ |
分析 如图所示，该几何体为三棱锥，其中底面ABC为等边三角形，侧棱PC⊥底面ABC．取AB的中点D，连接CD，PD，可得CD⊥AB，PD⊥AB．
解答 解：如图所示，该几何体为三棱锥，其中底面ABC为等边三角形，侧棱PC⊥底面ABC．
取AB的中点D，连接CD，PD，
则CD⊥AB，PD⊥AB，
CD=$\sqrt{3}$，PD=$\sqrt{P{C}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+（\sqrt{3}）^{2}}$=$\sqrt{7}$．
∴S△PAB=$\frac{1}{2}×\sqrt{7}×2$=$\sqrt{7}$．
故选：A．
点评 本题考查了三棱锥的三视图、三角形面积计算公式、空间位置关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
19．若实数x，y满足约束条件$\left\{\begin{array}{l}{x≤2}\\{y≤x}\\{x+y≥1}\end{array}\right.$，则z=3x+y的最大值为（ ）
| A． | 1 | B． | 2 | C． | 5 | D． | 8 |
20．集合P={x|x+$\frac{1}{x}$≤2，x∈Z}，集合Q={x|x2+2x-3＞0}，则P∩∁RQ=（ ）
| A． | [-3，0） | B． | {-3，-2，-1} | C． | {-3，-2，-1，0，1} | D． | {-3，-2，-1，1} |
17．
某学校对男女学生进行有关“习惯与礼仪”的调查，分别随机抽查了18名学生进行评分（百分制：得分越高，习惯与礼仪越好），评分记录如下：
男生：44，46，46，52，54，55，56，57，58，58，63，66，70，73，75，85，90，94．
女生：51，52，55，58，63，63，65，69，69，70，74，78，77，77，83，83，89，100
（1）请用茎叶图表示上面的数据，并通过茎叶图比较男女生“习惯与礼仪”评分的平均值及分散程度（不要求计算出具体的值，给出结论即可）．
（2）记评分在60分以下的等级为较差，评分在60分以上的等级为较好，请完成2×2列联表，并判断是否有95%的把握认为“习惯与礼仪”与性别有关？并说明理由．
附：
某学校对男女学生进行有关“习惯与礼仪”的调查，分别随机抽查了18名学生进行评分（百分制：得分越高，习惯与礼仪越好），评分记录如下：男生：44，46，46，52，54，55，56，57，58，58，63，66，70，73，75，85，90，94．
女生：51，52，55，58，63，63，65，69，69，70，74，78，77，77，83，83，89，100
（1）请用茎叶图表示上面的数据，并通过茎叶图比较男女生“习惯与礼仪”评分的平均值及分散程度（不要求计算出具体的值，给出结论即可）．
（2）记评分在60分以下的等级为较差，评分在60分以上的等级为较好，请完成2×2列联表，并判断是否有95%的把握认为“习惯与礼仪”与性别有关？并说明理由．
| 等级 性别 | 较差 | 较好 | 合计 |
| 男生 | |||
| 女生 | |||
| 合计 |
| P（K2≥k） | 0.050 | 0.010 | 0.001 | K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$ |
| k | 3.841 | 6.635 | 10.828 |
4．
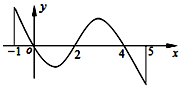已知函数f（x）定义域为[-1，5]，部分对应值如表，f（x）的导函数f′（x）的图象如图所示．
下列关于函数f（x）的命题：
①函数f（x）的极大值点有2个；
②函数f（x）在[0，2]上是减函数；
③若x∈[-1，t]时，f（x）的最大值是2，则t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
其中是真命题的是①②．（填写序号）
已知函数f（x）定义域为[-1，5]，部分对应值如表，f（x）的导函数f′（x）的图象如图所示．| x | -1 | 0 | 4 | 5 |
| f（x） | 1 | 2 | 2 | 1 |
①函数f（x）的极大值点有2个；
②函数f（x）在[0，2]上是减函数；
③若x∈[-1，t]时，f（x）的最大值是2，则t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
其中是真命题的是①②．（填写序号）
14．检验双向分类列联表数据下，两个分类特征（即两个因素变量）之间是彼此相关还是相互独立的问题，在常用的方法中，最为精确的做法是（ ）
| A． | 三维柱形图 | B． | 二维条形图 | C． | 等高条形图 | D． | 独立性检验 |
5．已知A（1，0，0）、B（0，1，0）、C（0，0，1），则平面ABC的一个单位法向量是（ ）
| A． | （$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$，-$\frac{\sqrt{3}}{3}$） | B． | （$\frac{\sqrt{3}}{3}$，-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$） | C． | （-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$） | D． | （-$\frac{\sqrt{3}}{3}$，-$\frac{\sqrt{3}}{3}$，-$\frac{\sqrt{3}}{3}$） |