题目内容

18．如图，三棱柱ABC-A1B1C1的侧面ABB1A1为正方形，侧面BB1C1C为菱形，∠CBB1=60°，AB⊥B1C
（1）求证：平面ABB1A1⊥平面BB1C1C；
（2）若AB=2，求三棱柱ABC-A1B1C1的高．

分析 （1）证明AB⊥BB1．AB⊥B1C，推出AB⊥平面BB1C1C，然后证明平面ABB1A1⊥BB1C1C．
（2）设O是BB1的中点，连结CO，则CO⊥BB1．求出CO，连结AB1，利用${V}_{{B}_{1}-ABC}$=${V}_{C-AB{B}_{1}}$求解三棱柱ABC-A1B1C1的高即可．

解答 （1）证明：由侧面ABB1A1为正方形，知AB⊥BB1．
又AB⊥B1C，BB1∩B1C=B1，所以AB⊥平面BB1C1C，
又AB?平面ABB1A1，所以平面ABB1A1⊥BB1C1C．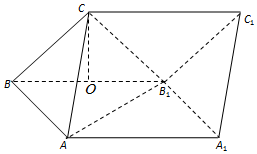
…（5分）
解：（2）设O是BB1的中点，连结CO，则CO⊥BB1．
由（1）知，CO⊥平面ABB1A1，且CO=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$…（7分）
连结AB1，则${V}_{C-AB{B}_{1}}$=$\frac{1}{3}$${S}_{△AB{B}_{1}}$•CO=$\frac{1}{6}$AB2•CO=$\frac{2\sqrt{3}}{3}$…（9分）
因${V}_{{B}_{1}-ABC}$=${V}_{C-AB{B}_{1}}$=$\frac{1}{3}×\frac{1}{2}×2×2×h$=$\frac{2\sqrt{3}}{3}$，则h=$\sqrt{3}$．
故三棱柱ABC-A1B1C1的高$\sqrt{3}$…（12分）

点评 本题考查空间几何体的距离的求法，等体积法的应用，直线与平面垂直的判定定理的应用，考查空间想象能力以及计算能力．

练习册系列答案
相关题目
11．已知点P（2，1）在圆C：x2+y2+ax-2y+b=0上，点P关于直线x+y-1=0的对称点也在圆C上，则圆C的圆心坐标为（　　）
A．（0，1）B．（1，0）C．（2，1）D．（1，2）
12．“经过两条相交直线有且只有一个平面”是（　　）
A．全称命题B．特称命题C．p∨q的形式D．p∧q的形式
6．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）离心率e=$\frac{\sqrt{2}}{2}$，过C（-1，0）点且斜率为1的直线l与椭圆交于A，B两点，且C点分有向线段$\overrightarrow{AB}$所成的比为3．
（1）求该椭圆方程；
（2）P，Q为椭圆上两动点，满足$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0，探求$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$是否为定值，并说明理由．
13．在区间[0，2]上随机地取一个数x，则事件“-1≤log ${\;}_{\frac{1}{2}}$（x+$\frac{1}{2}$）≤1”发生的概率（　　）
A．$\frac{1}{3}$B．$\frac{2}{3}$C．$\frac{3}{4}$D．$\frac{1}{4}$
3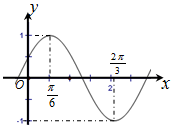．已知函数f（x）=Asin（ωx+φ）（A＞0，?＞0，|φ|＜$\frac{π}{2}$）的简图如下，则A，ω，φ分别为（　　）
A．1，2，-$\frac{π}{3}$B．1，$\frac{1}{2}$，-$\frac{π}{3}$C．1，2，$\frac{π}{6}$D．1，$\frac{1}{2}$，$\frac{π}{6}$
10．已知|AB|=3，A、B分别在x轴和y轴上滑动，O为坐标原点，$\overrightarrow{OP}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$，则动点P的轨迹方程是$\frac{{x}^{2}}{4}+{y}^{2}=1$．
7．若f（x）=ax3+3x2+2，f′（-1）=3，则a的值等于（　　）
A．5B．4C．3D．6
8．若变量x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≤8\\ 2y-x≤4\end{array}\right.$，且z=5y-x的最大值为a，最小值为b，则a-b的值是（　　）
A．16B．24C．30D．48

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网