题目内容
8．若变量x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≤8\\ 2y-x≤4\end{array}\right.$，且z=5y-x的最大值为a，最小值为b，则a-b的值是（ ）| A． | 16 | B． | 24 | C． | 30 | D． | 48 |
分析 作出可行域，变形目标函数可得y=$\frac{1}{5}$x+$\frac{1}{5}$z，平移直线y=$\frac{1}{5}$x，易得最大值和最小值，作差可得答案．
解答 解：作出变量x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≤8\\ 2y-x≤4\end{array}\right.$，所对应的可行域（如图阴影），
变形目标函数可得y=$\frac{1}{5}$x+$\frac{1}{5}$z，
平移直线y=$\frac{1}{5}$x，可知当直线经过点A（8，0）时，目标函数取最小值b=-8，
当直线经过点B（4，4）时，目标函数取最大值a=16，
∴a-b=16-（-8）=24
故选：B．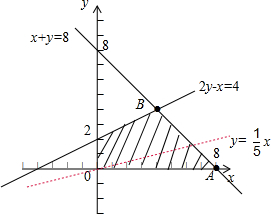
点评 本题考查简单线性规划的运用，注意运用数形结合的思想方法，以及平移法，准确作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
如图，三棱柱ABC-A1B1C1的侧面ABB1A1为正方形，侧面BB1C1C为菱形，∠CBB1=60°，AB⊥B1C
16．
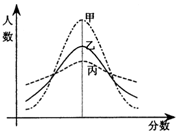某次市教学质量检测，甲、乙、丙三科考试成绩的直方图如图所示（由于人数众多，成绩分布的直方图可视为正态分布），则由图中曲线可得下列说法中正确的一个是（ ）
某次市教学质量检测，甲、乙、丙三科考试成绩的直方图如图所示（由于人数众多，成绩分布的直方图可视为正态分布），则由图中曲线可得下列说法中正确的一个是（ ）| A． | 甲、乙、丙的总体的平均数不相同 | B． | 乙科总体的标准差及平均数都居中 | ||
| C． | 丙科总体的平均数最小 | D． | 甲科总体的标准差最小 |
3．已知椭圆${C_1}：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$和圆${C_2}：{x^2}+{y^2}={b^2}$，若椭圆C1上存在点P，过点P作圆C2的两条切线PA，PB（A，B为对应的切点），且满足$∠APB=\frac{π}{3}$，则椭圆最圆的时离心率e=（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{2}}}{4}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{4}$ |
13．已知曲线y=$\frac{{x}^{2}}{2}$-3lnx的一条切线的与直线x+2y+10=0垂直，则切点的横坐标为（ ）
| A． | $\frac{1}{3}$ | B． | 2 | C． | 1 | D． | 3 |