题目内容
3.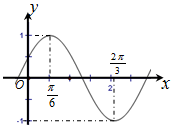 已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )
已知函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图如下,则A,ω,φ分别为( )| A. | 1,2,-$\frac{π}{3}$ | B. | 1,$\frac{1}{2}$,-$\frac{π}{3}$ | C. | 1,2,$\frac{π}{6}$ | D. | 1,$\frac{1}{2}$,$\frac{π}{6}$ |
分析 根据已知中函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的简图,分析函数的最值,周期,最大值点,进而可得A,ω,φ的值.
解答 解:∵函数f(x)=Asin(ωx+φ)(A>0,?>0,|φ|<$\frac{π}{2}$)的最大值为1,最小值为-1,
故A=1,
由$\frac{T}{2}$=$\frac{2π}{3}$-$\frac{π}{6}$=$\frac{π}{2}$,
故T=π=$\frac{2π}{ω}$,
故ω=2,
将x=$\frac{π}{6}$代入得:2×$\frac{π}{6}$+φ=$\frac{π}{2}$,
解得:φ=$\frac{π}{6}$,
故选:C.
点评 本题考查的知识点是函数f(x)=Asin(ωx+φ)的图象和性质,函数f(x)=Asin(ωx+φ)的解析式求法,难度中档.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
16.已知三点A(-1,-1),B(1,x),C(2,5)共线,则x的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.已知四边形ABCD为正方形,点E是CD的中点,若$\overrightarrow{AB}$=$\vec a$,$\overrightarrow{AD}$=$\vec b$,则$\overrightarrow{BE}$=( )
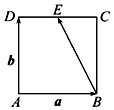

| A. | $\frac{1}{2}$$\vec b$+$\vec a$ | B. | $\vec b$$-\frac{1}{2}$$\vec a$ | C. | $\frac{1}{2}$$\vec a$+$\vec b$ | D. | $\vec a$-$\frac{1}{2}$$\vec b$ |
12.若集合M={y|y=$\frac{1}{{x}^{2}}$},N={x|y=$\sqrt{x-1}$},那么M∩N=( )
| A. | (0,+∞) | B. | (1,+∞) | C. | [1,+∞) | D. | [0,+∞) |
13.已知曲线y=$\frac{{x}^{2}}{2}$-3lnx的一条切线的与直线x+2y+10=0垂直,则切点的横坐标为( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | 1 | D. | 3 |
 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C