题目内容
已知函数f(x)=ex-a(x-1),其中,a∈R,e是自然对数的底数.
(1)当a=-1时,求函数f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性,并写出相应的单调区间;
(3)已知b∈R,若函数f(x)≥b对任意x∈R都成立,求ab的最大值.
(1)当a=-1时,求函数f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性,并写出相应的单调区间;
(3)已知b∈R,若函数f(x)≥b对任意x∈R都成立,求ab的最大值.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:计算题,函数的性质及应用,导数的概念及应用,导数的综合应用
分析:(1)求出a=-1的函数的导数,求出切线的斜率和切点,由点斜式方程即可得到;
(2)求出导数,讨论当a≤0时,当a>0时,令导数大于0,得增区间,令导数小于0,得减区间;
(3)由(2)可得,a>0时f(x)取得极小值也为最小值,由恒成立思想可得a(2-lna)≥b,则ab≤a2(2-lna),令t=a2(2-lna),求得导数,求出极大值也为最大值,即可得到.
(2)求出导数,讨论当a≤0时,当a>0时,令导数大于0,得增区间,令导数小于0,得减区间;
(3)由(2)可得,a>0时f(x)取得极小值也为最小值,由恒成立思想可得a(2-lna)≥b,则ab≤a2(2-lna),令t=a2(2-lna),求得导数,求出极大值也为最大值,即可得到.
解答:
解:(1)当a=-1时,f(x)=ex+x-1的导数为f′(x)=ex+1,
函数f(x)在点(1,f(1))处的切线斜率为e+1,
又切点为(1,e),则切线方程为y-e=(e+1)(x-1),即为(e+1)x-y-1=0;
(2)函数f(x)=ex-a(x-1)的导数f′(x)=ex-a,
当a≤0时,f′(x)>0,f(x)递增,则f(x)的增区间为(-∞,+∞);
当a>0时,f′(x)>0,解得,x>lna,f′(x)<0,解得,x<lna.
即有f(x)的增区间为(lna,+∞),减区间为(-∞,lna);
(3)由(2)可得,a≤0时,f(x)递增,无最值;
当a>0时,f(x)在(-∞,lna)上递减,在(lna,+∞)上递增,
则f(x)在x=lna处取得极小值也为最小值,且为a-a(lna-1)=a(2-lna).
函数f(x)≥b对任意x∈R都成立,则有a(2-lna)≥b,
则ab≤a2(2-lna),
令t=a2(2-lna),则t′=2a(2-lna)-a=a(3-2lna),
当0<a<e
时,t′>0,t递增;当a>e
时,t′<0,t递减.
则t在a=e
时取得极大,也为最大,且为e3(2-
)=
e3.
则ab的最大值为
e3.
函数f(x)在点(1,f(1))处的切线斜率为e+1,
又切点为(1,e),则切线方程为y-e=(e+1)(x-1),即为(e+1)x-y-1=0;
(2)函数f(x)=ex-a(x-1)的导数f′(x)=ex-a,
当a≤0时,f′(x)>0,f(x)递增,则f(x)的增区间为(-∞,+∞);
当a>0时,f′(x)>0,解得,x>lna,f′(x)<0,解得,x<lna.
即有f(x)的增区间为(lna,+∞),减区间为(-∞,lna);
(3)由(2)可得,a≤0时,f(x)递增,无最值;
当a>0时,f(x)在(-∞,lna)上递减,在(lna,+∞)上递增,
则f(x)在x=lna处取得极小值也为最小值,且为a-a(lna-1)=a(2-lna).
函数f(x)≥b对任意x∈R都成立,则有a(2-lna)≥b,
则ab≤a2(2-lna),
令t=a2(2-lna),则t′=2a(2-lna)-a=a(3-2lna),
当0<a<e
| 3 |
| 2 |
| 3 |
| 2 |
则t在a=e
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
则ab的最大值为
| 1 |
| 2 |
点评:本题考查导数的运用:求切线方程和求单调区间、极值和最值,考查分类讨论的思想方法,考查构造函数运用导数求最值的思想方法,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
为了解2000名学生对学校食堂的意见,准备从中抽取一个样本容量为50的样本.若采用系统抽样,则分段间隔k为( )
| A、20 | B、30 | C、40 | D、50 |
函数y=
的定义域是( )
| 1 |
| 2x-1 |
A、{x|x>
| ||
| B、{x|x≠0,x∈R} | ||
C、{x|x<
| ||
D、{x|x≠
|
过抛物线y2=8x的焦点F的直线交抛物线于A,B两点,交抛物线的准线与C,若|AF|=6,
=λ
,则λ的值为( )
| BC |
| FB |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
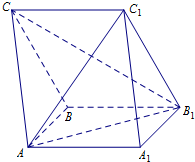 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.