题目内容
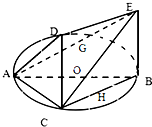 如图,一简单几何体ABCDE的一个面ABC内接于圆O,G、H分别是AE、BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,一简单几何体ABCDE的一个面ABC内接于圆O,G、H分别是AE、BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.(Ⅰ)证明:GH∥平面ACD;
(Ⅱ)若AC=BC=BE=2,求二面角O-CE-B的余弦值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,二面角的平面角及求法
专题:空间角
分析:(Ⅰ)连结GO,OH,证明GO∥平面ACD,OH∥平面ACD,利用平面与平面平行的判定定理证明平面GOH∥平面ACD.然后证明GH∥平面ACD.
(Ⅱ)以CB为x轴,CB为y轴,CD为z轴,建立如图所示的直角坐标系,求出C,B,A(,O,E的坐标,平面BCE的法向量
,平面OCE的法向量
.二面角O-CE-B是锐二面角,记为θ,利用空间向量的数量积求解cosθ即可.
(Ⅱ)以CB为x轴,CB为y轴,CD为z轴,建立如图所示的直角坐标系,求出C,B,A(,O,E的坐标,平面BCE的法向量
| m |
| n |
解答:

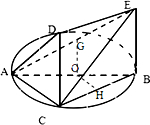 解:(Ⅰ)证明:连结GO,OH
解:(Ⅰ)证明:连结GO,OH
∵GO∥AD,OH∥AC…(2分)
∴GO∥平面ACD,OH∥平面ACD,又GO交HO于O…(.4分)
∴平面GOH∥平面ACD…(5分)
∴GH∥平面ACD…(6分)
(Ⅱ)以CB为x轴,CA为y轴,CD为z轴,建立如图所示的直角坐标系
则C(0,0,0),B(2,0,0),A(0,2,0),O(1,1,0),E(2,0,2)
平面BCE的法向量
=(0,1,0),设平面OCE的法向量
=(x0.y0.z0).…(8分)
=(2,0,2),
=(1,1,0).
∴
则
,
令x0=-1,∴
=(-1,1,1).…(10分)
∵二面角O-CE-B是锐二面角,记为θ,则
cosθ=|cos<
,
>|=
=
=
…(12分)

 解:(Ⅰ)证明:连结GO,OH
解:(Ⅰ)证明:连结GO,OH∵GO∥AD,OH∥AC…(2分)
∴GO∥平面ACD,OH∥平面ACD,又GO交HO于O…(.4分)
∴平面GOH∥平面ACD…(5分)
∴GH∥平面ACD…(6分)
(Ⅱ)以CB为x轴,CA为y轴,CD为z轴,建立如图所示的直角坐标系
则C(0,0,0),B(2,0,0),A(0,2,0),O(1,1,0),E(2,0,2)
平面BCE的法向量
| m |
| n |
| CE |
| CO |
∴
|
|
令x0=-1,∴
| n |
∵二面角O-CE-B是锐二面角,记为θ,则
cosθ=|cos<
| m |
| n |
| ||||
|
|
| 1 | ||
1×
|
| ||
| 3 |
点评:本题考查直线与平面平行的判定定理的证明,二面角的平面角的求法,考查空间想象能力以及计算能力.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知函数f(x)=
-lnx,则有下列结论中错误的是( )
| lnx |
| 1+x |
| A、?x0∈R,f(x)=0 | ||
| B、若x0是f(x)的最大值点,则f(x0)=x0 | ||
C、若x0是f(x)的最大值点,则f(x0)<
| ||
| D、若x0是f(x)的极大值点,则f(x)在(x0,+∞)上单调递增 |
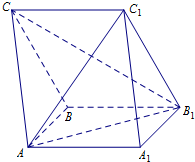 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.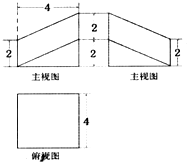 棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
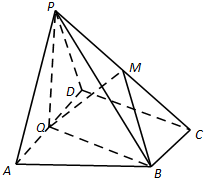 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=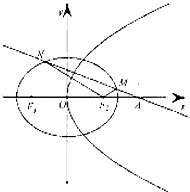 如图,己知椭圆C:
如图,己知椭圆C: