题目内容
已知圆心C在x轴上的圆过点A(2,2)和B(4,0).
(1)求圆C的方程;
(2)求过点M(4,6)且与圆C相切的直线方程;
(3)已知线段PQ的端点Q的坐标为(3,5),端点P在圆C上运动,求线段PQ的中点N的轨迹.
(1)求圆C的方程;
(2)求过点M(4,6)且与圆C相切的直线方程;
(3)已知线段PQ的端点Q的坐标为(3,5),端点P在圆C上运动,求线段PQ的中点N的轨迹.
考点:轨迹方程,圆的切线方程
专题:直线与圆
分析:(1)由已知求出线段AB的垂直平分线方程,令y=0,得x=2,即可求得圆心为C(2,0).然后由两点间的距离公式求得圆的半径,则圆C的方程可求.或设出圆心为C(a,0),由|AC|=|BC|求得a,则圆心坐标可求,再由半径r=|BC|=|4-2|=2.则圆的方程可求;
(2)由(1)知圆C的圆心坐标为C(2,0),半径r=2,然后分与圆C相切的直线的斜率不存在和斜率存在求得与圆C相切的直线方程;
(3)设点N的坐标为(x,y),P点的坐标为(x0,y0).由中点坐标公式把P的坐标用N的坐标表示,然后代入圆C的方程求得点N的轨迹方程.
(2)由(1)知圆C的圆心坐标为C(2,0),半径r=2,然后分与圆C相切的直线的斜率不存在和斜率存在求得与圆C相切的直线方程;
(3)设点N的坐标为(x,y),P点的坐标为(x0,y0).由中点坐标公式把P的坐标用N的坐标表示,然后代入圆C的方程求得点N的轨迹方程.
解答:
解:(1)线段AB的中点坐标为M(3,1),斜率为kAB=
=-1,
∴线段AB的垂直平分线方程为y-1=x-3,即为y=x-2.
令y=0,得x=2,即圆心为C(2,0).
由两点间的距离公式,得r=
=2.
∴适合题意的圆C的方程为(x-2)2+y2=4.
或:设圆心为C(a,0),由|AC|=|BC|得
=
,
解得a=2,∴圆心为C(2,0).
又半径r=|BC|=|4-2|=2.
∴适合题意的圆C的方程为(x-2)2+y2=4;
(2)由(1)知圆C的圆心坐标为C(2,0),半径r=2,
(i)当过点M(4,6)且与圆C相切的直线的斜率不存在时,其切线方程为x=4.
(ii)当过点M(4,6)且与圆C相切的直线的斜率存在时,
设为k,则切线方程为kx-y-4k+6=0.
由圆心到切线的距离等于半径,得
=2,解得k=
,
∴切线方程为
x-y-4×
+6=0,即4x-3y+2=0.
因此,过点M(4,6)且与圆C相切的直线方程为x=4或4x-3y+2=0;
(3)设点N的坐标为(x,y),P点的坐标为(x0,y0).
由于Q点的坐标为(3,5)且N为PQ的中点,∴x=
,y=
,
于是有x0=2x-3,y0=2y-5 ①,
∵P在圆C上运动,∴有(x0-2)2+
=4,
将①代入上式得(2x-3)2+(2y-5)2=4,即(x-
)2+(y-
)2=1.
∴点N的轨迹是以(
,
)为圆心,半径为1的圆.
| 0-2 |
| 4-2 |
∴线段AB的垂直平分线方程为y-1=x-3,即为y=x-2.
令y=0,得x=2,即圆心为C(2,0).
由两点间的距离公式,得r=
| (2-2)2+22 |
∴适合题意的圆C的方程为(x-2)2+y2=4.
或:设圆心为C(a,0),由|AC|=|BC|得
| (a-2)2+22 |
| (a-4)2 |
解得a=2,∴圆心为C(2,0).
又半径r=|BC|=|4-2|=2.
∴适合题意的圆C的方程为(x-2)2+y2=4;
(2)由(1)知圆C的圆心坐标为C(2,0),半径r=2,
(i)当过点M(4,6)且与圆C相切的直线的斜率不存在时,其切线方程为x=4.
(ii)当过点M(4,6)且与圆C相切的直线的斜率存在时,
设为k,则切线方程为kx-y-4k+6=0.
由圆心到切线的距离等于半径,得
| |2k-4k+6| | ||
|
| 4 |
| 3 |
∴切线方程为
| 4 |
| 3 |
| 4 |
| 3 |
因此,过点M(4,6)且与圆C相切的直线方程为x=4或4x-3y+2=0;
(3)设点N的坐标为(x,y),P点的坐标为(x0,y0).
由于Q点的坐标为(3,5)且N为PQ的中点,∴x=
| 3+x0 |
| 2 |
| 5+y0 |
| 2 |
于是有x0=2x-3,y0=2y-5 ①,
∵P在圆C上运动,∴有(x0-2)2+
| y | 2 0 |
将①代入上式得(2x-3)2+(2y-5)2=4,即(x-
| 3 |
| 2 |
| 5 |
| 2 |
∴点N的轨迹是以(
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题考查了圆的方程的求法,考查了圆的切线方程的求法,训练了利用代入法求曲线的轨迹方程,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知b>a>0,ab=2,则
的取值范围是( )
| a2+b2 |
| a-b |
| A、(-∞,-4] |
| B、(-∞,-4) |
| C、(-∞,-2] |
| D、(-∞,-2) |
过抛物线y2=8x的焦点F的直线交抛物线于A,B两点,交抛物线的准线与C,若|AF|=6,
=λ
,则λ的值为( )
| BC |
| FB |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
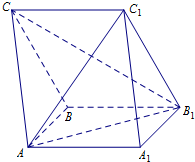 如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.
如图所示,在三棱柱ABC-A1B1C1中,AA1B1B为正方形,BB1C1C是菱形,平面AA1B1B⊥平面BB1C1C.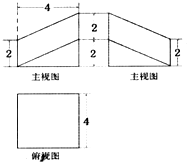 棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
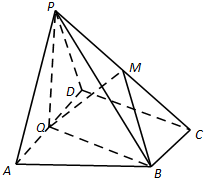 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=