题目内容
15.若实数x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$,则z=x-2y的最大值是( )| A. | 2 | B. | 1 | C. | 0 | D. | -4 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合可得最优解,求出最优解的坐标,代入目标函数得答案.
解答 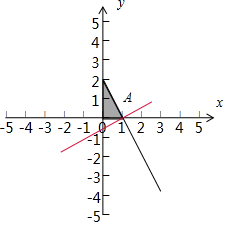 解:由约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$,作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$,作出可行域如图,
化目标函数z=x-2y为直线方程的斜截式y=$\frac{1}{2}$x-$\frac{z}{2}$.
由图可知,当直线y=$\frac{1}{2}$x-$\frac{z}{2}$过点A时,直线在y轴上的截距最小,z最大,为z=1-2×0=1.
故选:B.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
6.对于函数f(x),若在定义域内存在实数x0,满足f(-x0)=-f(x0),则称f(x)为“局部奇函数”,已知f(x)=4x-m2x+1+m-3为定义R上的“局部奇函数”,则实数m的取值范围是( )
| A. | $[1-\sqrt{3},+∞)$ | B. | [-2,+∞) | C. | $[-2,2\sqrt{2}]$ | D. | $[-2,1+\sqrt{3}]$ |
3.抛物线C:y2=4x的焦点为F,N为准线上一点,M为y轴上一点,∠MNF为直角,若线段MF的中点E在抛物线C上,则△MNF的面积为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $3\sqrt{2}$ |
20.已知$z=\frac{3i}{1-i}$,则复数z的虚部为( )
| A. | $-\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}i$ | D. | $\frac{3}{2}i$ |
7.i是虚数单位,则$\frac{2i}{1+3i}$=( )
| A. | -$\frac{3}{5}$+$\frac{1}{5}$i | B. | $\frac{3}{4}$-$\frac{1}{4}$i | C. | $\frac{3}{5}$+$\frac{1}{5}$i | D. | $\frac{3}{4}$+$\frac{1}{4}$i |
4.“a=$\frac{1}{18}$“是“对任意的正数x,x+$\frac{a}{2x}$≥$\frac{1}{3}$“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
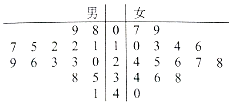 某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”. .
. 的值;
的值; 的值.
的值.