题目内容
10.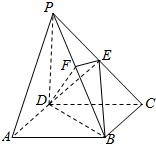 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.(Ⅰ)求证:PA∥平面EDB;
(Ⅱ)求证:PB⊥平面EFD;
(Ⅲ)求异面直线BE与PA所成角的大小.
分析 (I)以点D为坐标原点,DA、DC、DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,连接AC,AC交BD于点G,连接EG.分别求出PA,EG的方向向量,易判断PA与EG平行,进而由线面平行的判定定理得到答案.
(II)分别求出DE与PB的方向向量,由它们的数量积为0,易得DE⊥PB,再由EF⊥PB结合线面垂直的判定定理即可得到答案.
(III)求出$\overrightarrow{BE}$=(-2,-1,1),$\overrightarrow{PA}$=(2,0,-2),即可求异面直线BE与PA所成角的大小.
解答  (I)证明:如图,以点D为坐标原点,DA、DC、DP所在直线分别为x轴、y轴、z轴,
(I)证明:如图,以点D为坐标原点,DA、DC、DP所在直线分别为x轴、y轴、z轴,
建立空间直角坐标系,得以下各点坐标:D(0,0,0),A(2,0,0),B(2,2,0),
C(0,2,0),P(0,0,2)…(1分)
连接AC,AC交BD于点G,连接EG.∵底面ABCD是正方形,∴G为AC的中点.G点坐标为(1,1,0).
又E为PC的中点,E点坐标为(0,1,1),
∴$\overrightarrow{PA}$=(2,0,-2),$\overrightarrow{EG}$=(1,0,-1)
∴$\overrightarrow{PA}$=2$\overrightarrow{EG}$
∴PA∥EG
∵EG?平面EDB,PA?平面EDB,
∴PA∥平面EDB
(II)证明:∵$\overrightarrow{PB}$=(2,2,-2),$\overrightarrow{DE}$=(0,1,1)
∴$\overrightarrow{PB}$•$\overrightarrow{DE}$=0
∴PB⊥DE
又∵DE⊥PB,EF⊥PB,DE∩EF=E,
∴PB⊥平面EFD.
(III)解:∵$\overrightarrow{BE}$=(-2,-1,1),$\overrightarrow{PA}$=(2,0,-2),
∴|cos<$\overrightarrow{BE}$,$\overrightarrow{PA}$>|=|$\frac{-6}{\sqrt{6}×2\sqrt{2}}$|=$\frac{\sqrt{3}}{2}$,
∴异面直线BE与PA所成角的大小为30°.
点评 本题考查的知识点是用空间向量求平面间的夹角,直线与平面平行的判定,直线与平面垂直的判定,二面角的平面角及求法,其中几何法的关键是熟练掌握空间直线与平面位置关系的定义、判定、性质及几何特征,建立良好的空间想像能力,几何法的关键是建立适当的空间坐标系,将空间线面关系及线面夹角问题转化为向量夹角问题.

| A. | x${\;}^{\frac{1}{2}}$ | B. | x${\;}^{\frac{9}{2}}$ | C. | x${\;}^{\frac{3}{2}}$ | D. | x${\;}^{\frac{2}{3}}$ |
| A. | f(x)=x-1 | B. | f(x)=x${\;}^{\frac{1}{2}}$ | C. | f(x)=x2 | D. | f(x)=x3 |
| A. | 1 | B. | 4 | C. | 3 | D. | 2 |
| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |
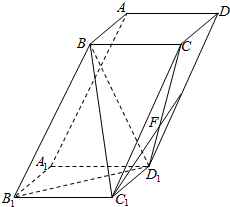 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,且B1C1=$\sqrt{2}$,BB1=BC1=BD1=$\sqrt{5}$.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,且B1C1=$\sqrt{2}$,BB1=BC1=BD1=$\sqrt{5}$.