题目内容
20.△ABC中,角A、B、C的对边分别为a、b、c.已知a2+c2-ac=b2.(1)求角B;
(2)当b=6,sinC=2sinA时,求△ABC的面积.
分析 (1)由余弦定理变形已知式子可得cosB,结合三角形内角的范围可得;
(2)由题意正弦定理可得c=2a,代入a2+c2-ac=b2可解得$a=2\sqrt{3}$,$c=4\sqrt{3}$,可得△ABC为直角三角形,由三角形的面积公式可得.
解答 解:(1)∵△ABC中a2+c2-ac=b2,∴ac=a2+c2-b2,
∴由余弦定理可得$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{ac}{2ac}=\frac{1}{2}$,
∵B为三角形的内角,∴$B=\frac{π}{3}$;
(2)∵sinC=2sinA,∴由正弦定理可得c=2a,
代入a2+c2-ac=b2得36=a2+4a2-2a2,
解得$a=2\sqrt{3}$,$c=4\sqrt{3}$,
满足a2+b2=c2,∴△ABC为直角三角形,
∴${S_{△ABC}}=\frac{1}{2}•2\sqrt{3}•6=6\sqrt{3}$
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-2y+2≥0}\\{x≤2}\end{array}\right.$,若目标函数z=ax+y(a>0)取得最小值时的最优解有无穷个,则实数a等于( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
8.已知点P(3,4),Q(2,6),向量$\overrightarrow{EF}$=(-1,λ),若$\overrightarrow{PQ}$•$\overrightarrow{EF}$=0,则实数λ的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
15.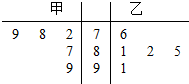 将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
 将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )| A. | x甲<x乙,乙比甲成绩稳定 | B. | x甲>x乙;甲比乙成绩稳定 | ||
| C. | x甲>x乙;乙比甲成绩稳定 | D. | x甲<x乙;甲比乙成绩稳定 |
5.在正方体ABCD-A1B1C1D1中,直线DC1与平面A1BD所成角的余弦值是( )
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
9.已知a、b∈R,且满足0<a<1<b,则下列大小关系正确的是( )
| A. | ab<ba<logab | B. | ba<logab<ab | C. | logab<ba<ab | D. | logab<ab<ba |
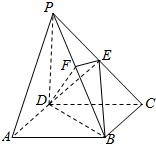 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.