题目内容
15.已知函数$f(x)=\left\{\begin{array}{l}x+2,x≤0\\ 1gx,x>0\end{array}\right.$,则函数y=|f(x)|-1的零点个数是( )| A. | 1 | B. | 4 | C. | 3 | D. | 2 |
分析 问题转化成f(x)=1或f(x)=-1.当x>0时,可解得x=10或x=$\frac{1}{10}$;当x≤0时,可解得x=-1或x=-3,即方程有4个根,则函数有4个零点.
解答 解:由y=|f(x)|-1=0得|f(x)|=1,即f(x)=1或f(x)=-1.
当x>0时,由lgx=1或lgx=-1,解得x=10或x=$\frac{1}{10}$.
当x≤0时,由x+2=1或x+2=-1,解得x=-1或x=-3.
所以函数y=|f(x)|-1的零点个数是4个,
故选B
点评 本题考查根的存在性及根的个数的判断,转化为对应方程的根是解决问题的关键,属中档题.

练习册系列答案
相关题目
3.函数y=e|lnx|的图象大致为( )
| A. | 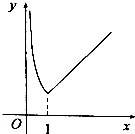 | B. | 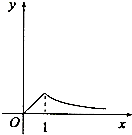 | C. | 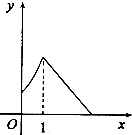 | D. | 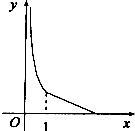 |
7.设a为正实数,i为虚数单位,z=a-i,若|z|=2,则a=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | -$\sqrt{2}$ | D. | 1 |
5.在正方体ABCD-A1B1C1D1中,直线DC1与平面A1BD所成角的余弦值是( )
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
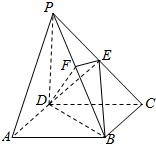 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.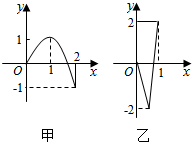 如图,定义在[-2,2]上的偶函数f(x)和定义在[-1,1]上的奇函数g(x)的部分图象分别如图甲、乙,则函数y=f(g(x))的零点个数为( )
如图,定义在[-2,2]上的偶函数f(x)和定义在[-1,1]上的奇函数g(x)的部分图象分别如图甲、乙,则函数y=f(g(x))的零点个数为( )