题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{4x-4,x≤1}\\{{x}^{2}-4x+3,x>1}\end{array}\right.$,g(x)=lnx,则函数y=f(x)-g(x)的零点个数为( )| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
分析 在同一坐标系中画出函数函数f(x)与函数y=lnx的图象,两函数图象交点的个数即为函数y=f(x)-g(x)的零点的个数.
解答  解:令g(x)=f(x)-lnx=0得f(x)=lnx
解:令g(x)=f(x)-lnx=0得f(x)=lnx
∴函数g(x)=f(x)-lnx的零点个数即为函数f(x)与函数y=lnx的图象的交点个数,
在同一坐标系中画出函数f(x)与函数y=lnx的图象,如图所示,
由图象知函数y=f(x)-lnx上有3个零点.
故选:C.
点评 此题是中档题.考查函数零点与函数图象交点之间的关系,体现了转化的思想和数形结合的思想,体现学生灵活应用图象解决问题的能力.

练习册系列答案
相关题目
17.函数y=|log2x|-2-x的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.设a为正实数,i为虚数单位,z=a-i,若|z|=2,则a=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | -$\sqrt{2}$ | D. | 1 |
14.已知集合M={x|-1<x<1},N={y|y=sinx,x∈[0,$\frac{π}{2}$]},则M∩N=( )
| A. | (-1,1) | B. | [-1,1] | C. | (-1,0] | D. | [0,1) |
11.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-2y+2≥0}\\{x≤2}\end{array}\right.$,若目标函数z=ax+y(a>0)取得最小值时的最优解有无穷个,则实数a等于( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
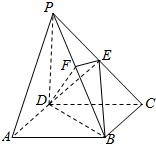 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.