题目内容
5.下列函数中,与y=$\frac{{e}^{x}-{e}^{-x}}{2}$的奇偶性和单调性都相同的是( )| A. | f(x)=x-1 | B. | f(x)=x${\;}^{\frac{1}{2}}$ | C. | f(x)=x2 | D. | f(x)=x3 |
分析 先判断出y=x的奇偶性和单调性,再根据指数函数、二次函数、幂函数的奇偶性和单调性,依次判断出个选项中函数的奇偶性和单调性,可得答案.
解答 解:函数y=$\frac{{e}^{x}-{e}^{-x}}{2}$是奇函数,且在R上是单调递增函数,
A、f(x)=x-1是奇函数,且在R上不是单调递增函数,故A不正确;
B、f(x)=${x}^{\frac{1}{2}}$不是奇函数,故B不正确;
C、f(x)=x2是偶函数,故C不正确;
D、f(x)=x3,则x∈R,又f(-x)=-x3=-f(x),所以此函数是奇函数,y=x3在R上是增函数,故D正确,
故选D.
点评 本题考查了函数的奇偶性和单调性判断方法,此题的关键是熟练掌握基本初等函数的奇偶性和单调性.

练习册系列答案
相关题目
17.函数y=|log2x|-2-x的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.已知集合M={x|-1<x<1},N={y|y=sinx,x∈[0,$\frac{π}{2}$]},则M∩N=( )
| A. | (-1,1) | B. | [-1,1] | C. | (-1,0] | D. | [0,1) |
15.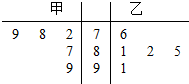 将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
 将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )
将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是( )| A. | x甲<x乙,乙比甲成绩稳定 | B. | x甲>x乙;甲比乙成绩稳定 | ||
| C. | x甲>x乙;乙比甲成绩稳定 | D. | x甲<x乙;甲比乙成绩稳定 |
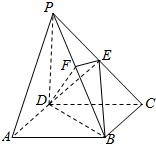 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.