题目内容
1.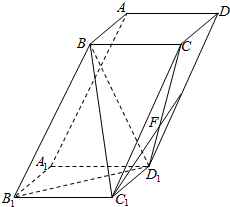 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,且B1C1=$\sqrt{2}$,BB1=BC1=BD1=$\sqrt{5}$.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,且B1C1=$\sqrt{2}$,BB1=BC1=BD1=$\sqrt{5}$.(1)求证:平面B1BD1⊥平面A1B1C1D1;
(2)已知E为棱DD1的中点,线段C1E与线段CD1的交于点F,求直线A1F与平面BB1D1所成角的正弦值.
分析 (1)连接A1C1,则A1C1∩B1D1=O,连接BO,证明BO⊥平面A1B1C1D1,即可证明平面B1BD1⊥平面A1B1C1D1;
(2)建立如图所示的坐标系,则平面BB1D1的法向量为(1,0,0),求出$\overrightarrow{{A}_{1}F}$,即可求直线A1F与平面BB1D1所成角的正弦值.
解答 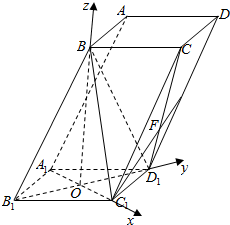 (1)证明:连接A1C1,则A1C1∩B1D1=O,连接BO,
(1)证明:连接A1C1,则A1C1∩B1D1=O,连接BO,
∵BB1=BC1=BD1=$\sqrt{5}$.
∴BO⊥B1D1,BO⊥A1C1,
∵A1C1∩B1D1=O,
∴BO⊥平面A1B1C1D1,
∵BO?平面B1BD1,
∴平面B1BD1⊥平面A1B1C1D1;
(2)解:由题意,建立如图所示的坐标系,则平面BB1D1的法向量为(1,0,0),A1(-1,0,0),
∵E(0,$\frac{3}{2}$,1),C1(-1,0,0),C1F=$\frac{2}{3}$C1E,
∴F(-$\frac{1}{3}$,1,$\frac{2}{3}$),
∴$\overrightarrow{{A}_{1}F}$=($\frac{2}{3}$,1,$\frac{2}{3}$),
∴直线A1F与平面BB1D1所成角的正弦值为|$\frac{\frac{2}{3}}{\sqrt{\frac{4}{9}+1+\frac{4}{9}}}$|=$\frac{2\sqrt{17}}{17}$.
点评 本题考查平面与平面垂直的判定,考查线面角,考查学生分析解决问题的能力,考查向量方法的运用,属于中档题.

练习册系列答案
相关题目
11.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+2y-2≥0}\\{x-2y+2≥0}\\{x≤2}\end{array}\right.$,若目标函数z=ax+y(a>0)取得最小值时的最优解有无穷个,则实数a等于( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
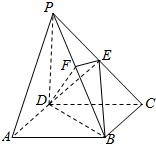 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=DC=2,点E为PC的中点,EF⊥PB,垂足为F点.