如图.在△ABC中.∠BAC=90°.AB=AC=2.E是边BC的中点.D是边AC上一动点.则$\overrightarrow{AE}$•$\overrightarrow{BD}$的取值范围是( )A．[0.2]B．[-2.0]C．[0.2$\sqrt{2}$]D．[-2$\sqrt{2}$.0] 题目和参考答案——青夏教育精英家教网—

题目内容

18．

如图，在△ABC中，∠BAC=90°，AB=AC=2，E是边BC的中点，D是边AC上一动点，则$\overrightarrow{AE}$•$\overrightarrow{BD}$的取值范围是（　　）

A．

[0，2]

B．

[-2，0]

C．

[0，2$\sqrt{2}$]

D．

[-2$\sqrt{2}$，0]

分析根据题意建立平面直角坐标系，利用坐标表示向量$\overrightarrow{AE}$、$\overrightarrow{BD}$，
再求出数量积$\overrightarrow{AE}$•$\overrightarrow{BD}$的取值范围．

解答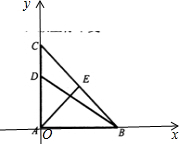解：根据题意，建立平面直角坐标系如图所示；
则A（0，0），B（2，0），C（0，2），E（1，1），
设D（0，y），则0≤y≤2；
∴$\overrightarrow{AE}$=（1，1），$\overrightarrow{BD}$=（-2，y），
∴$\overrightarrow{AE}$•$\overrightarrow{BD}$=1×（-2）+y=y-2；
由y∈[0，2]，得y-2∈[-2，0]，
∴$\overrightarrow{AE}$$•\overrightarrow{BD}$的取值范围是[-2，0]．
故选：B．

点评本题考查了平面向量的数量积运算问题，利用坐标系表示平面向量的坐标是解题的关键．

练习册系列答案

9．函数$f（x）=sin（2x+\frac{π}{3}）$给出下列结论正确的是（　　）

	A．	f（x）在$（\frac{π}{12}，\frac{2π}{3}）$是减函数		B．	$f（x-\frac{π}{6}）$是奇函数
	C．	f（x）的一个对称中心为$（\frac{π}{6}，0）$		D．	f（x）的一条对称轴为$x=\frac{π}{6}$

6．若函数f（x）=lg（10^x+1）+ax是偶函数，g（x）=$\frac{{4}^{x}-b}{{2}^{x}}$是奇函数，则a+b的值是（　　）

13．已知复数Z=$\frac{{i}^{2017}}{1+i}$（i是虚数单位），则复数Z的共轭复数是（　　）

A．

1+i

B．