题目内容
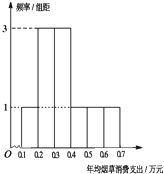 某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题:
某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题:(Ⅰ)在该地区随机抽取3个人,求其中至少1人吸烟的概率;
(Ⅱ)据统计,烟草消费税大约为烟草消费支出的40%,该地区为居民支付因吸烟导致的疾病治疗等各种费用年均约为18800万元.问:当地烟草消费税是否足以支付当地居民因吸烟导致的疾病治疗等各种费用?说明理由.
考点:频率分布直方图,众数、中位数、平均数
专题:计算题,概率与统计
分析:(I)地区吸烟者人数占总人数的
,可得抽取1人,吸烟的概率为
,不吸烟的概率为
,利用独立重复事件发生的概率公式计算抽取的3个人都不吸烟的概率,再求其对立事件发生的概率;
(II)吸烟者烟草消费支出的平均数为各个小矩形底边中点的横坐标乘以对应小矩形的面积之和,求得吸烟者烟草消费支出的平均数,
根据烟草消费税的比例求得地区年均烟草消费税,比较与18800万元的大小,可得答案.
| 1 |
| 8 |
| 1 |
| 8 |
| 7 |
| 8 |
(II)吸烟者烟草消费支出的平均数为各个小矩形底边中点的横坐标乘以对应小矩形的面积之和,求得吸烟者烟草消费支出的平均数,
根据烟草消费税的比例求得地区年均烟草消费税,比较与18800万元的大小,可得答案.
解答:
解:(Ⅰ)由题意可知,该地区吸烟者人数占总人数的
,
∴抽取的3个人中至少1人吸烟的概率为P=1-
(
)0×(
)3=1-
=
;
(Ⅱ)由频率分布直方图可知,吸烟者烟草消费支出的平均数为0.15×0.1+0.25×0.3+0.35×0.3+0.45×0.1+0.55×0.1+0.65×0.1=0.36(万元),
又该地区吸烟者人数为
×100万,
∴该地区年均烟草消费税为
×100×104×0.36×0.4=18000(万元),
∵该地区因吸烟导致的疾病治疗等各种费用约为18800万元,它超过了当地烟草消费税,
∴当地的烟草消费税不足以支付当地居民因吸烟导致的疾病治疗等各种费用.
| 1 |
| 8 |
∴抽取的3个人中至少1人吸烟的概率为P=1-
| C | 0 3 |
| 1 |
| 8 |
| 7 |
| 8 |
| 343 |
| 512 |
| 169 |
| 512 |
(Ⅱ)由频率分布直方图可知,吸烟者烟草消费支出的平均数为0.15×0.1+0.25×0.3+0.35×0.3+0.45×0.1+0.55×0.1+0.65×0.1=0.36(万元),
又该地区吸烟者人数为
| 1 |
| 8 |
∴该地区年均烟草消费税为
| 1 |
| 8 |
∵该地区因吸烟导致的疾病治疗等各种费用约为18800万元,它超过了当地烟草消费税,
∴当地的烟草消费税不足以支付当地居民因吸烟导致的疾病治疗等各种费用.
点评:本题考查了由频率分布直方图求样本的平均数,考查了独立重复事件发生的概率,考查了利用概率统计知识解决实际应用问题,考查数据处理能力、运算求解能力以及应用用意识,计算要细心.

练习册系列答案
相关题目
某几何体的俯视图是正方形,则该几何体不可能是( )
| A、圆柱 | B、圆锥 |
| C、三棱柱 | D、四棱柱 |

 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.