题目内容
{an}各项均为正的等比数列，已知a3+a4-a2-a1=8，求a5+a6+a7+a8最小值．
考点：等比数列的性质
专题：导数的概念及应用,等差数列与等比数列
分析：可判数列{an+an+1}也是各项均为正的等比数列，设数列{an+an+1}的公比为x，a1+a2=a，则x∈（1，+∞），a3+a4=ax，结合已知可得a=
，代入可得y=a5+a6+a7+a8=ax2+ax3=
，x∈（1，+∞），由导数求函数的最值即可．
| 8 |
| x-1 |
| 8(x3+x2) |
| x-1 |
解答：
解：∵数列{an}是各项均为正的等比数列，
∴数列{an+an+1}也是各项均为正的等比数列，
设数列{an+an+1}的公比为x，a1+a2=a，
则x∈（1，+∞），a3+a4=ax，
∴有a3+a4-a2-a1=ax-a=8，即a=
∴y=a5+a6+a7+a8=ax2+ax3=
，x∈（1，+∞），
求导数可得y′=
，令y′＞0可得x＞
，
故函数在（1，
）单调递减，（
，+∞）单调递增，
∴当x=
时，y=a5+a6+a7+a8取最小值：44+20
．
∴数列{an+an+1}也是各项均为正的等比数列，
设数列{an+an+1}的公比为x，a1+a2=a，
则x∈（1，+∞），a3+a4=ax，
∴有a3+a4-a2-a1=ax-a=8，即a=
| 8 |
| x-1 |
∴y=a5+a6+a7+a8=ax2+ax3=
| 8(x3+x2) |
| x-1 |
求导数可得y′=
| 16x(x2-x-1) |
| (x-1)2 |
| ||
| 2 |
故函数在（1，
| ||
| 2 |
| ||
| 2 |
∴当x=
| ||
| 2 |
| 5 |
点评：本题考查等比数列的性质，涉及导数的应用，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数h（x）=2sin（2x+
）的图象与函数f（x）的图象关于点（0，1）对称，则函数f（x）可由h（x）经过怎样的变换得到（ ）
| π |
| 4 |
A、向上平移2个单位，向右平移
| ||
B、向上平移2个单位，向左平移
| ||
C、向下平移2个单位，向右平移
| ||
D、向下平移2个单位，向左平移
|
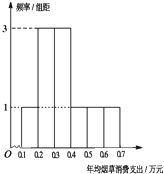某地区共有100万人，现从中随机抽查800人，发现有700人不吸烟，100人吸烟．这100位吸烟者年均烟草消费支出情况的频率分布直方图如图．将频率视为概率，回答下列问题：