题目内容
已知向量|
|=2,|
|=1,
•
=1,则向量
与
-
的夹角为 .
| a |
| b |
| a |
| b |
| a |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意可得
•(
-
),由模长公式可得|
-
|,代入夹角公式计算可得夹角的余弦值,可得夹角.
| a |
| a |
| b |
| a |
| b |
解答:
解:由题意可得
•(
-
)=
2-
•
=3,
|
-
|=
=
=
,
∴cos<
,
-
>=
=
=
,
∴向量
与
-
的夹角为与
-
的夹角为
,
故答案为:
.
| a |
| a |
| b |
| a |
| a |
| b |
|
| a |
| b |
(
|
|
| 3 |
∴cos<
| a |
| a |
| b |
| ||||||
|
|
| 3 | ||
2×
|
| ||
| 2 |
∴向量
| a |
| a |
| b |
| a |
| b |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查平面向量的数量积的运算,涉及向量的夹角公式和模长公式,属中档题.

练习册系列答案
相关题目
设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2014)2f(x+2014)-4f(-2)>0的解集为( )
| A、(-∞,-2012) |
| B、(-2012,0) |
| C、(-∞,-2016) |
| D、(-2016,0) |
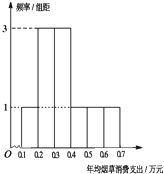 某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题:
某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题: