题目内容
 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.(Ⅰ)请在图中补全频率分布直方图;
(Ⅱ)若B大学决定在成绩高的第4,5组中用分层抽样的方法抽取6名学生,并且分成2组,每组3人进行面试,求95分(包括95分)以上的同学在同一个小组的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(Ⅰ)根据等差数列的性质计算出各组人数,从而求出各组频率,即可补全频率分布直方图;
(Ⅱ)列举抽样的所有可能,找出符合题意得基本事件个数,利用概率个数计算即可.
(Ⅱ)列举抽样的所有可能,找出符合题意得基本事件个数,利用概率个数计算即可.
解答:
 解:(Ⅰ)∵第四组的人数为60,
解:(Ⅰ)∵第四组的人数为60,
∴总人数为:5×60=300,
由直方图可知,
第五组人数为:0.02×5×300=30人,
又∵
=15为公差,
∴第一组人数为:45人,
第二组人数为:75人,
第三组人数为:90人.
∴第1至第4组的频率分别为:0.15,0.25,0.30,0.20.
如图可补全频率分布直方图.
(Ⅱ)第四组中抽取人数:
×60=4人,
第五组中抽取人数:
×30=2人,
∴95分以上的共2人.
设第四组抽取的四人为A1,A2,A3,A4,
第五组抽取的2人为B1,B2,
这六人分成两组有两种情况,
情况一:B1,B2在同一小组有4种可能结果,
情况二:B1,B2不在同一小组有6种可能结果,
总共10种可能结果,
∴两人在一组的概率为
=
.
 解:(Ⅰ)∵第四组的人数为60,
解:(Ⅰ)∵第四组的人数为60,∴总人数为:5×60=300,
由直方图可知,
第五组人数为:0.02×5×300=30人,
又∵
| 60-30 |
| 2 |
∴第一组人数为:45人,
第二组人数为:75人,
第三组人数为:90人.
∴第1至第4组的频率分别为:0.15,0.25,0.30,0.20.
如图可补全频率分布直方图.
(Ⅱ)第四组中抽取人数:
| 6 |
| 90 |
第五组中抽取人数:
| 6 |
| 90 |
∴95分以上的共2人.
设第四组抽取的四人为A1,A2,A3,A4,
第五组抽取的2人为B1,B2,
这六人分成两组有两种情况,
情况一:B1,B2在同一小组有4种可能结果,
情况二:B1,B2不在同一小组有6种可能结果,
总共10种可能结果,
∴两人在一组的概率为
| 4 |
| 10 |
| 2 |
| 5 |
点评:本题考查等差数列性质与频率分布直方图的综合应用,古典概型概率的计算,属于中档题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
函数h(x)=2sin(2x+
)的图象与函数f(x)的图象关于点(0,1)对称,则函数f(x)可由h(x)经过怎样的变换得到( )
| π |
| 4 |
A、向上平移2个单位,向右平移
| ||
B、向上平移2个单位,向左平移
| ||
C、向下平移2个单位,向右平移
| ||
D、向下平移2个单位,向左平移
|
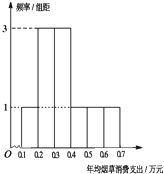 某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题:
某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题: