题目内容
计算:
(1)
(1+
)2×
(2)
(1+
)2×
(3)
[(
)2+1]×
(4)
[(
)2+1]×
.
(1)
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
(2)
| lim |
| n→∞ |
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
(3)
| lim |
| n→∞ |
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
(4)
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
考点:极限及其运算
专题:点列、递归数列与数学归纳法
分析:(1)利用等差数列的前n项和公式及公式[12+22+…+n2=
]即可得出;
(2)利用(1)和极限的运算性质即可得出;
(4)利用等差数列的前n项和公式及公式[12+22+…+n2=
]即可得出;
(3)利用(4)和极限的运算性质即可得出.
| n(n+1)(2n+1) |
| 6 |
(2)利用(1)和极限的运算性质即可得出;
(4)利用等差数列的前n项和公式及公式[12+22+…+n2=
| n(n+1)(2n+1) |
| 6 |
(3)利用(4)和极限的运算性质即可得出.
解答:
解:(1)∵(1+
)2=1+
+(
)2,
∴
(1+
)2×
=
[n+n+1+
]=
(2+
)(7+
).
(2)由(1)可得
(1+
)2×
=
×2×7=
.
(4)
[(
)2+1]×
=[
+n]×
=
[(1+
)(2+
)+1].
(3)由(4)可得
[(
)2+1]×
=
(1×2+1)=
.
| i |
| n |
| 2i |
| n |
| i |
| n |
∴
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
| 1 |
| n |
| n(n+1)(2n+1) |
| 6n2 |
| 1 |
| 6 |
| 1 |
| n |
| 1 |
| n |
(2)由(1)可得
| lim |
| n→∞ |
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
| 1 |
| 6 |
| 7 |
| 3 |
(4)
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
| n(n+1)(2n+1) |
| 6n2 |
| 1 |
| n |
| 1 |
| 6 |
| 1 |
| n |
| 1 |
| n |
(3)由(4)可得
| lim |
| n→∞ |
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
| 1 |
| 6 |
| 1 |
| 2 |
点评:本题考查了等差数列的前n项和公式及公式[12+22+…+n2=
]、极限的运算性质等基础知识与基本技能方法,属于中档题.
| n(n+1)(2n+1) |
| 6 |

练习册系列答案
相关题目
设xi∈N(i=1,2,3,4,5,6…),则满足x1<x2<x3<x4<10的有序数组(x1,x2,x3,x4)的个数为( )
| A、126 | B、3024 |
| C、210 | D、5040 |
 唐徕回中随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100],
唐徕回中随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100],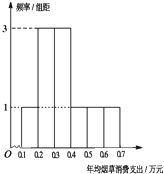 某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题:
某地区共有100万人,现从中随机抽查800人,发现有700人不吸烟,100人吸烟.这100位吸烟者年均烟草消费支出情况的频率分布直方图如图.将频率视为概率,回答下列问题: