题目内容
已知函数f（x）=|x-3|-5，g（x）=|x+2|-2．
（Ⅰ）求不等式f（x）≤2的解集；
（Ⅱ）若不等式f（x）-g（x）≥m-3有解，求实数m的取值范围．
（Ⅰ）求不等式f（x）≤2的解集；
（Ⅱ）若不等式f（x）-g（x）≥m-3有解，求实数m的取值范围．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：（Ⅰ）由题意得f（x）≤2，得|x-3|≤7，利用绝对值的意义化为-7≤x-3≤7，解得即可；
（II）f（x）-g（x）≥m-3有解?|x-3|-|x+2|≥m有解?（|x-3|-|x+2|）max≥m，利用绝对值的意义求出|x-3|-|x-2|的最大值即可．
（II）f（x）-g（x）≥m-3有解?|x-3|-|x+2|≥m有解?（|x-3|-|x+2|）max≥m，利用绝对值的意义求出|x-3|-|x-2|的最大值即可．
解答：
解：（Ⅰ）由题意得f（x）≤2，得|x-3|≤7，
∴-7≤x-3≤7，解得-4≤x≤10，
∴x的取值范围是[-4，10]．
（Ⅱ）∵f（x）-g（x）≥m-3有解，
∴|x-3|-|x+2|≥m有解，
∵||x-3|-|x+2||≤|（x-3）-（x+2）|=5，
∴-5≤|x-3|-|x+2|≤5
∴m≤5，即m的取值范围是（-∞，5]．
∴-7≤x-3≤7，解得-4≤x≤10，
∴x的取值范围是[-4，10]．
（Ⅱ）∵f（x）-g（x）≥m-3有解，
∴|x-3|-|x+2|≥m有解，
∵||x-3|-|x+2||≤|（x-3）-（x+2）|=5，
∴-5≤|x-3|-|x+2|≤5
∴m≤5，即m的取值范围是（-∞，5]．
点评：本题考查了绝对值的意义及其性质和不等式，考查了数形结合的能力，属于中档题．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
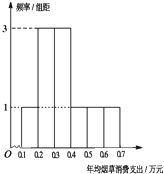某地区共有100万人，现从中随机抽查800人，发现有700人不吸烟，100人吸烟．这100位吸烟者年均烟草消费支出情况的频率分布直方图如图．将频率视为概率，回答下列问题：