题目内容
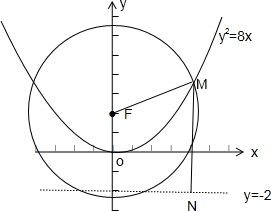
设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设F到准线的距离d1,M(x0,y0)到准线的距离d2,依题意,d1=4,d2=y0+2,且d2>d1,从而可得答案.
解答:
解:∵抛物线C:x2=8y的焦点F(0,2),准线方程为:y=-2,
设F到准线的距离d1,M(x0,y0)到准线的距离d2,
则d1=4,d2=y0+2=|FM|(抛物线定义),
依题意得:|FM|>d1=4,
即y0+2>4,
解得:y0>2.
∴y0的取值范围是(2,+∞).
故答案为:(2,+∞).
设F到准线的距离d1,M(x0,y0)到准线的距离d2,

则d1=4,d2=y0+2=|FM|(抛物线定义),
依题意得:|FM|>d1=4,
即y0+2>4,
解得:y0>2.
∴y0的取值范围是(2,+∞).
故答案为:(2,+∞).
点评:本题考查抛物线的简单性质,着重考查抛物线定义的应用,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
函数y=-
x2+2x-5的图象的对称轴是( )
| 1 |
| 2 |
| A、直线x=2 |
| B、直线a=-2 |
| C、直线y=2 |
| D、直线x=4 |
 已知圆O:x2+y2=m(m>0)与抛物线y2=ax(a>0)相交于A(1,1),B(1,-1)两点.
已知圆O:x2+y2=m(m>0)与抛物线y2=ax(a>0)相交于A(1,1),B(1,-1)两点.