题目内容
已知平面向量
,
满足|
|=|
|=2,(
+2
)•(
-
)=-2,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设
与
的夹角为θ,由题意可得4+2×2×cosθ-2×4=-2,解得cosθ的值,再结合θ∈[0,π],求得θ的值.
| a |
| b |
解答:
解:设
与
的夹角为θ,由题意可得
2+
•
-2b2=-2,
即4+2×2×cosθ-2×4=-2,解得cosθ=
.
再结合θ∈[0,π],∴θ=
,
故选:B.
| a |
| b |
| a |
| a |
| b |
即4+2×2×cosθ-2×4=-2,解得cosθ=
| 1 |
| 2 |
再结合θ∈[0,π],∴θ=
| π |
| 3 |
故选:B.
点评:本题主要考查两个向量的数量积的定义,根据三角函数的值求角,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、直角坐标系中横、纵坐标相等的点能够组成一个集合 |
| B、π∈{x|x<3,x∈R} |
| C、∅={0} |
| D、{(1,2)}⊆{1,2,3} |
已知集合M={x|x<1},集合N={y|y>0},则M∩N=( )
| A、{x|x<1} |
| B、{x|x>1} |
| C、{x|0<x<1} |
| D、∅ |
在复平面内,复数z=
(i为虚数单位)的共轭复数等于( )
| 3-i |
| 1+i |
| A、1+2i | B、1-2i |
| C、1+3i | D、-1-3i |
如果直线3x-
y+m=0与双曲线C:
-
=1(a>0,b>0)恒有两个公共点,则双曲线C的离心率的取值范围是( )
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) |
| B、(2,+∞) |
| C、(1,2] |
| D、[2,+∞) |
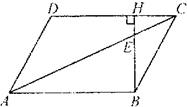 如图,在平行四边形ABCD中,BH⊥CD于点H,BH交AC于点E,已知|
如图,在平行四边形ABCD中,BH⊥CD于点H,BH交AC于点E,已知| 如图,已知直线l1:y=4x+m,(m<0)与抛物线
如图,已知直线l1:y=4x+m,(m<0)与抛物线