题目内容
20. 如图,在四棱锥A-BECD中,已知底面BECD是平行四边形,且CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.
如图,在四棱锥A-BECD中,已知底面BECD是平行四边形,且CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.(Ⅰ)求证:平面ABD⊥平面BECD;
(Ⅱ)求点E到平面ACD的距离.
分析 (Ⅰ)取AD中点O,连结OC,OA,证明AO⊥平面BECD,即可证明平面ABD⊥平面BECD;
(Ⅱ)利用等体积转化,即可求点E到平面ACD的距离.
解答 (Ⅰ)证明:取AD中点O,连结OC,OA.
∵BO=DO,AB=AD,
∴AO⊥BD,∵BO=DO,BC=CD,∴CO⊥BD,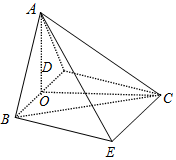
在△AOC中,由已知可得AO=1,CO=$\sqrt{3}$,
而AC=2,∴AO2+CO2=AC2.
∴∠AOC=90°,即AO⊥OC.
∵BD∩OC=O,∴AO⊥平面BECD.
又 OA?平面ABD,
所以平面ABD⊥平面BCD;
(Ⅱ)解:设点E到平面ACD的距离为h.∵VE-ACD=VA-CDE,∴$\frac{1}{3}$h•S△ACD=$\frac{1}{3}$•AO•S△CDE.
在△ACD中,CA=CD=2,AD=$\sqrt{2}$,∴S△ACD=$\frac{\sqrt{7}}{2}$.
而AO=1,${S_{△CDE}}={S_{△BCD}}=\frac{{\sqrt{3}}}{4}×{2^2}=\sqrt{3}$,∴h=$\frac{AO•S△CDE}{S△ACD}$=$\frac{{\sqrt{3}}}{{\;\frac{{\sqrt{7}}}{2}\;}}=\frac{{2\sqrt{21}}}{7}$.
∴点E到平面ACD的距离为$\frac{{2\sqrt{21}}}{7}$.
点评 本题考查线面垂直,平面与平面垂直的证明,考查点E到平面ACD的距离,正确计算体积是关键.

练习册系列答案
相关题目
10.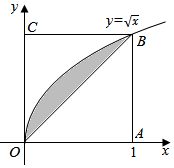 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)等于( )
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)等于( )
 如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)等于( )
如图所示,在边长为1的正方形OABC内任取一点P,用A表示事件“点P恰好自由曲线$y=\sqrt{x}$与直线x=1及x轴所围成的曲边梯形内”,B表示事件“点P恰好取自阴影部分内”,则P(B|A)等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
12.已知1,x,y,z,9成等比数列,则y=( )
| A. | -3 | B. | 3 | C. | 5 | D. | ±3 |
9.函数y=cosx-(sinx)2+2的值域为( )
| A. | [1,3] | B. | [$\frac{1}{2}$,$\frac{11}{4}$] | C. | [$\frac{3}{4}$,3] | D. | [$\frac{3}{4}$,$\frac{11}{4}$] |