题目内容
已知数列{an}的前n项和为Sn,且Sn=n2,n∈N*.
(1)求数列{an}的通项公式;
(2)设bn=
,n∈N*,求数列{bn}的前n项和Tn.
(3)设An=(1+
)(1+
)(1+
)•…•(1+
),n∈N*,试比较An与
的大小,并证明你的结论.
(1)求数列{an}的通项公式;
(2)设bn=
| 1 |
| anan+1 |
(3)设An=(1+
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| an+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)当n≥2时,an=Sn-Sn-1=2n-1,当n=1时,a1=S1=1,即可得出.
(2)bn=
=
(
-
),利用“裂项求和”即可得出数列{bn}的前n项和Tn.
(3)利用1+
=1+
=
>
=
,即可得出An>
.
(2)bn=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
(3)利用1+
| 1 |
| an |
| 1 |
| 2n-1 |
| 2n-1+2n+1 |
| 2(2n-1) |
| ||
| 2n-1 |
|
| an+1 |
解答:
解:(1)当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
当n=1时,a1=S1=1,上式也成立,
∴an=2n-1.
(2)bn=
=
=
(
-
),
∴数列{bn}的前n项和Tn=
[(1-
)+(
-
)+…+(
-
)]=
(1-
)=
.
(3)∵1+
=1+
=
=
>
=
,
∴An>
×
×
×…×
=
=
.
∴An>
.
当n=1时,a1=S1=1,上式也成立,
∴an=2n-1.
(2)bn=
| 1 |
| anan+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴数列{bn}的前n项和Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
(3)∵1+
| 1 |
| an |
| 1 |
| 2n-1 |
| 2n |
| 2n-1 |
| 2n-1+2n+1 |
| 2(2n-1) |
| ||
| 2n-1 |
|
∴An>
|
|
|
|
| 2n+1 |
| an+1 |
∴An>
| an+1 |
点评:本题考查了递推式的应用、“裂项求和”、不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
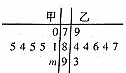 如图为甲,乙两名学生7次考试成绩的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙考试成绩的平均数分别为a和b,则一定有( )
如图为甲,乙两名学生7次考试成绩的茎叶图(其中m为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙考试成绩的平均数分别为a和b,则一定有( )| A、a>b |
| B、a<b |
| C、a=b |
| D、a,b的大小与m的值有关 |
设向量
,
,
满足
+
+
=
,且
•
=0,则|
|=3,|
|=4,则|
|=( )
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| a |
| c |
| b |
| A、5 | ||
B、
| ||
C、
| ||
| D、7 |
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),且当x>2时,f(x)单调递增,如果x1+x2<4,且(x1-2)(x2-2)<0,则下列说法正确的是( )
| A、f(x1)+f(x2)的值为正数 |
| B、f(x1)+f(x2)的值为负数 |
| C、f(x1)+f(x2)的值正负不能确定 |
| D、f(x1)+f(x2)的值一定为零 |
如果实数x、y满足条件
,那么z=4x•2-y的最大值为( )
|
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
