题目内容
函数y=f(x)是定义在R上的奇函数且y=f(x+1)也是奇函数,若f(3)=0,则函数y=f(x)在区间(0,8)内的零点个数至少有( )
| A、4 | B、5 | C、6 | D、7 |
考点:函数零点的判定定理
专题:计算题
分析:由题意知f(-x)=-f(x),f(x)=-f(-x+2);从而可得f(x)为周期为2的函数,从而确定零点的个数.
解答:
解:∵函数y=f(x)是定义在R上的奇函数,
∴f(-x)=-f(x);
又∵y=f(x+1)也是奇函数,
∴f(x+1)=-f(-x+1),
则f(x)=-f(-x+2);
故f(x)=-f(-x)=-(-f(x+2))
=f(x+2);
故f(x)为周期为2的函数,
由f(3)=0知,
f(2)=f(0)=0;
故f(1)=f(2)=…=f(7)=0;
故函数y=f(x)在区间(0,8)内的零点个数至少有7个;
故选D.
∴f(-x)=-f(x);
又∵y=f(x+1)也是奇函数,
∴f(x+1)=-f(-x+1),
则f(x)=-f(-x+2);
故f(x)=-f(-x)=-(-f(x+2))
=f(x+2);
故f(x)为周期为2的函数,
由f(3)=0知,
f(2)=f(0)=0;
故f(1)=f(2)=…=f(7)=0;
故函数y=f(x)在区间(0,8)内的零点个数至少有7个;
故选D.
点评:本题考查了函数的性质应用及函数的零点个数的判断,属于基础题.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
若复数z=
,则z为( )
| 1-i |
| 1+i |
| A、i | B、-i | C、2i | D、1+i |
若a,b,c依次表示方程2x+x=1,log2x+x=1,log2x+x=2的根,则a,b,c的大小顺序为( )
| A、c<a<b |
| B、a<b<c |
| C、a<c<b |
| D、c<b<a |
对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[-1.08]=-2,已知函数f(x)=x-[x],则下列结论中正确的是( )
A、f(sin
| ||||
B、方程f(x)=
| ||||
| C、f(x)是周期函数 | ||||
| D、f(x)是增函数 |
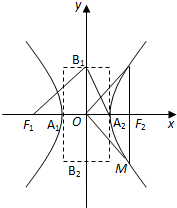 我们把离心率为e=
我们把离心率为e=
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
①双曲线x2-
| 2y2 | ||
|
②若b2=ac,则该双曲线是黄金双曲线;
③若∠F1B1A2=90°,则该双曲线是黄金双曲线;
④若∠MON=90°,则该双曲线是黄金双曲线.
| A、①② | B、①③ |
| C、①③④ | D、①②③④ |
设x,y满足约束条件
( )
|
| A、6 | ||
B、
| ||
| C、7 | ||
D、
|