题目内容
计算：
．
2sin50°+
| ||||
| cos20° |
考点：三角函数的化简求值
专题：计算题,三角函数的求值
分析：将原式中的“切”化“弦”后，通分，约分后逆用两角差的余弦，可得原式=
，再逆用两角和的正弦与诱导公式即可求得答案．
2sin50°+2
| ||
| cos20° |
解答：
解：原式=
=
=
=
=
=
=4×
=4．
2sin50°+
| ||||
| cos20° |
=
2sin50°+2
| ||||||||
| cos20° |
=
2sin50°+2
| ||
| cos20° |
=
4(
| ||||||
| cos20° |
=
| 4sin(50°+60°) |
| cos20° |
=
| 4sin(90°+20°) |
| cos20° |
=4×
| cos20° |
| cos20° |
点评：本题考查三角函数的化简求值，考查两角和的正弦与两角差的余弦，考查转化思想与运算求值的能力，属于中档题．
练习册系列答案
相关题目
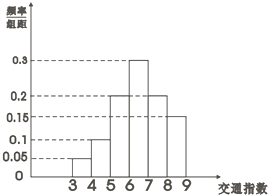交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T．其范围为[0，10]，分别有五个级别：T∈[0，2）畅通；T∈[2，4）基本畅通； T∈[4，6）轻度拥堵； T∈[6，8）中度拥堵；T∈[8，10]严重拥堵，晚高峰时段，从某市交通指挥中心选取了市区20个交通路段，依据其交通指数数据绘制直方图如图所示．