题目内容
4.在ABC中,若cosA=$\frac{4}{5}$,C=120°,BC=2$\sqrt{3}$,则AB=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由同角三角函数基本关系可得sinA,再由正弦定理可得AB=$\frac{BCsinC}{sinA}$,代值计算可得.
解答 解:∵在ABC中cosA=$\frac{4}{5}$,C=120°,BC=2$\sqrt{3}$,
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{3}{5}$,
由正弦定理可得AB=$\frac{BCsinC}{sinA}$=$\frac{2\sqrt{3}×\frac{\sqrt{3}}{2}}{\frac{3}{5}}$=5
故选:C
点评 本题考查正弦定理解三角形,涉及同角三角函数基本关系,属基础题.

练习册系列答案
相关题目
14.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点到一条渐近线的距离等于焦距的$\frac{1}{4}$,则该双曲线的离心率为( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{2\sqrt{3}}{3}$ |
15.已知直线y=1-x与双曲线ax2+by2=1(a>0,b<0)的渐近线交于A,B两点,且过原点和线段AB中点的直线的斜率为$-\frac{{\sqrt{3}}}{2}$,则$\frac{a}{b}$的值为( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{2\sqrt{3}}}{3}$ | C. | $-\frac{{9\sqrt{3}}}{2}$ | D. | $-\frac{{2\sqrt{3}}}{27}$ |
12.已知实数x,y满足条件$\left\{\begin{array}{l}y≤x\\ x+y≥2\\ 2x+y≥6\end{array}\right.$,则z=3x+2y的取值范围是( )
| A. | (-∞,10] | B. | [5,10] | C. | [8,+∞) | D. | [8,10] |
19.执行如图所示的程序框图,若输入A的值为2,则输出的n值为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
9.阅读如图的程序框图,运行相应的程序,输出的结果为( )
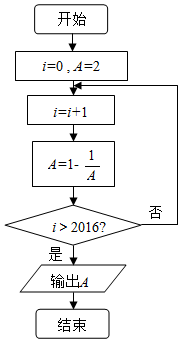

| A. | -2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2 |
16.若全集U=R,集合A={x|1<2x<4},B={x|x-1>0},则A∩(∁UB)=( )
| A. | {x|0<x≤1} | B. | {x|1<x<2} | C. | {x|0<x<1} | D. | {x|1≤x<2} |
13.设不等式组$\left\{\begin{array}{l}{x-y+4≥0}\\{x+y≥0}\\{x≤1}\end{array}\right.$表示的平面区域为Ω1,不等式组$\left\{\begin{array}{l}{-2≤x≤1}\\{-1≤y≤5}\end{array}\right.$表示的平面区域为Ω2,在区域Ω2内随机取一点,则该点是取自于区域Ω1的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
14.已知Sn为数列{an}的前n项和,且a1=1,a2=3,an+2=3an,则S2016=( )
| A. | 2×(31008-1) | B. | 2×31008 | C. | $\frac{{{3^{2016}}-1}}{2}$ | D. | $\frac{{{3^{2016}}+1}}{2}$ |