题目内容
已知
=（1，-1），
=（λ，1），
与
的夹角为钝角，则λ的取值范围是（ ）
| a |
| b |
| a |
| b |
| A、λ＞1 |
| B、λ＜1 |
| C、λ＜-1 |
| D、λ＜-1或-1＜λ＜1 |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：根据平面向量的数量积公式进行计算即可得到结论．
解答：
解：若
与
的夹角为钝角，
则
•
＜0，即λ-1＜0，
∴λ＜1，
当
与
反向共线时，由
=x
，x＜0时，
即
，解得x=-1且λ=-1，
此时
与
的夹角为π，不是钝角，不满足条件，
∴λ≠-1，
综上λ＜-1或-1＜λ＜1，
故选：D．
| a |
| b |
则
| a |
| b |
∴λ＜1，
当
| a |
| b |
| a |
| b |
即
|
此时
| a |
| b |
∴λ≠-1，
综上λ＜-1或-1＜λ＜1，
故选：D．
点评：本题主要考查平面向量的应用，利用夹角和数量积之间的关系是解决本题的关键，注意要去掉向量共线的情况．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，内角A，B，C的对边分别为a，b，c，已知acosB+bcosA=csinC，b2+c2-a2=
bc，则B=（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
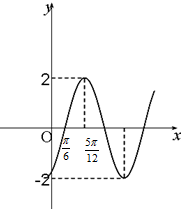函数f（x）=2sin（ωx+φ），（ω＞0，-| π |
| 2 |
| π |
| 2 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向右平移
| ||||
D、向右平移
|
等差数列{an}中，a1=7，a3=3，前n项和为Sn，则n=（ ）时，Sn取到最大值．
| A、4或5 | B、4 | C、3 | D、2 |
有如下四个命题：
①命题“若x2-3x+2=0，则x=1“的逆否命题为“若x≠1，则x2-3x+2≠0”．
②若x=y=0，则x2+y2=0的逆命题是真命题．
③若p∧q为假命题，则p，q均为假命题．
④命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”．
其中错误命题的个数是（ ）
①命题“若x2-3x+2=0，则x=1“的逆否命题为“若x≠1，则x2-3x+2≠0”．
②若x=y=0，则x2+y2=0的逆命题是真命题．
③若p∧q为假命题，则p，q均为假命题．
④命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”．
其中错误命题的个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
在数列{an}中，a1，a2，a3，…，an满足an+1-2an=0，a1＞0，则（ ）
| A、a1+s8-s7＞3a4 |
| B、a1+s8-s7＜3a4 |
| C、a1+s8-s7=3a4 |
| D、a1+s8-s7与3a4的大小关系不能由已知条件确定 |