题目内容
2.直线y=a分别与曲线y=2(x+1),y=x+lnx交于A、B,则|AB|的最小值为$\frac{3}{2}$.分析 设A(x1,a),B(x2,a),则2(x1+1)=x2+lnx2,表示出x1,求出|AB|,利用导数求出|AB|的最小值.
解答 解:设A(x1,a),B(x2,a),则2(x1+1)=x2+lnx2,
∴x1=$\frac{1}{2}$(x2+lnx2)-1,
∴|AB|=x2-x1=$\frac{1}{2}$(x2-lnx2)+1,
令y=$\frac{1}{2}$(x-lnx)+1,则y′=$\frac{1}{2}$(1-$\frac{1}{x}$),
∴函数在(0,1)上单调递减,在(1,+∞)上单调递增,
∴x=1时,函数的最小值为$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查导数知识的运用,考查学生分析解决问题的能力,正确求导确定函数的单调性是关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
12.曲线C1的参数方程为$\left\{\begin{array}{l}x=\sqrt{10}cosθ\\ y=sinθ\end{array}$(θ为参数),圆C2:x2+(y-6)2=2,设P,Q分别为曲线C1和圆C2上的点,则P,Q两点间的最大距离是( )
| A. | 5$\sqrt{2}$ | B. | $\sqrt{46}$+$\sqrt{2}$ | C. | 7+$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
10.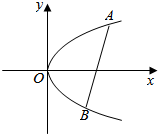 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )| A. | 2p | B. | $\frac{5}{2}p$ | C. | $\frac{3}{2}p$ | D. | 3p |
7.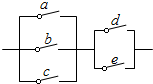 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
14.已知直线l1:y=ax+1与l2:y=$\sqrt{3}$x+2互相垂直,则a=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
11.有编号为A1,A2,…,A9的9道题,其难度系数如表:
其中难度系数小于0.50的为难题.
(Ⅰ)从上述9道题中,随机抽取1道,求这道题为难题的概率;
(Ⅱ)从难题中随机抽取2道,求这两道题目难度系数相等的概率.
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 |
| 难度系数 | 0.48 | 0.56 | 0.52 | 0.37 | 0.69 | 0.47 | 0.47 | 0.58 | 0.50 |
(Ⅰ)从上述9道题中,随机抽取1道,求这道题为难题的概率;
(Ⅱ)从难题中随机抽取2道,求这两道题目难度系数相等的概率.