题目内容
在1,2,…,2006中随机选取三个数,能构成递增等差数列的概率是 .
考点:古典概型及其概率计算公式
专题:计算题,概率与统计
分析:由古典概型概率公式求解,注意能构成递增等差数列的三个数的总个数.
解答:
解:由题意,符合古典概型,
一共的情况有
,
成立的情况有1002+1002+1001+1001+…1+1=2×
=1002×1003,
则能构成递增等差数列的概率P=
=
.
故答案为:
.
一共的情况有
| c | 3 2006 |
成立的情况有1002+1002+1001+1001+…1+1=2×
| (1002+1)×1002 |
| 2 |
则能构成递增等差数列的概率P=
| 3×2×1×1003×1002 |
| 2006×2005×2004 |
| 3 |
| 4010 |
故答案为:
| 3 |
| 4010 |
点评:本题考查了古典概型概率公式,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
已知{an}是等差数列,a1+a2=4,a7+a8=28,则该数列前8项和S8等于( )
| A、72 | B、64 |
| C、100 | D、120 |
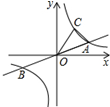 如图,已知直线y=
如图,已知直线y=