Question

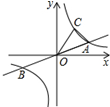如图，已知直线y=

1

2

x与双曲线y=

k

x

（k＞0）交于A、B两点，点B的坐标为（-4，-2），C为双曲线y=

k

x

（k＞0）上一点，且在第一象限内，若△AOC面积为6，则点C的坐标为

 

．

Answer 1

考点：幂函数的性质,一次函数的性质与图象

专题：函数的性质及应用

分析：把点B的坐标（-4，-2）代入双曲线y=

k

x

，可得k=8，双曲线方程为y=

8

x

．联立

y= 1 2 x xy=8

，取x＞0，解得A（4，2）．设C（x，

8

x

）．（x＞0）．点C到直线y=

1

2

x的距离h=

|x- 16 x |

5

．利用△AOC面积6=

1

2

|OA|h即可得出．

解答： 解：把点B的坐标（-4，-2）代入双曲线y=

k

x

，可得k=-4×（-2）=8．
∴双曲线方程为y=

8

x

．
联立

y= 1 2 x xy=8

，取x＞0，解得x=4，y=2．
∴A（4，2）．
设C（x，

8

x

）．（x＞0）
则点C到直线y=

1

2

x的距离h=

|x- 16 x |

5

．
|OA|=

42+22

=2

5

．
∴△AOC面积6=

1

2

|OA|h=

1

2

×2

5

×

|x- 16 x |

5

，
化为x²-16=±6x，x＞0．
解得x=2或8．
∴C（2，4）或（8，1）．

点评：本题考查了双曲线的方程及其性质、直线与双曲线相交转化为方程联立、点到直线的距离公式、三角形的面积计算公式、两点之间的距离公式，考查了计算能力，属于中档题．