题目内容

当a＞0且a≠1时，函数f（x）=ax+2必过定点
 
．
考点：指数函数的单调性与特殊点
专题：函数的性质及应用
分析：令x=0求得f（x）=a0+2=3，可得函数的图象经过得定点的坐标．
解答： 解：令x=0可得f（x）=a0+2=3，
可得函数的图象经过点（0，3），
故答案为：（0，3）．
点评：本题主要考查指数函数的单调性和特殊点，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
2x+1，x＜1
x2+ax，x≥1
，若f[f（0）]=4a，则
∫
2
1
a
x
dx=（　　）
A、2ln2
B、
1
3
ln2
C、ln2
D、9ln2
函数y=x（x2-1）的大致图象是（　　）
A、
B、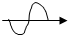
C、
D、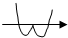
已知点A（-2，0），B（1，0），平面内的动点P满足|PA|=λ|PB|（λ为常数，λ＞0）．
（1）求点P的轨迹E的方程，并指出其表示的曲线的形状．
（2）当λ=2时，P的轨迹E与x轴交于C、D两点，M是轨迹上异于C、D的任意一点，直线l：x=-3，直线CM与直线l交于点C′，直线DM与直线l交于点D'．求证：以C′D′为直径的圆总过定点，并求出定点坐标．
如图是川东地区的行政区划，其中南充、达州各有8个交通
单位，广安、巴中各有6个交通单位（每个县有一个交通单位）．2012年底，四川省交通厅在川东地区用分层抽样的方法确定14个交通单位对该地区进行交通安全和交通执法大检查，则渠县被检查的概率为
 
．
∫
3
2
1
2
(2x+
1
x2
)dx=
 
．
已知等比数列{an}的公比q=
1
2
，其前4项和S4=60，则a2等于（　　）
A、8B、12C、16D、20
解方程或求值．
（1）解方程（
1
3
） 1-X2•9X=9；     
（2）求值：lg5lg20-lg2lg50-lg25．
设x∈R，向量
a
=(x，1)，
b
=(1，-2)，若|
a
+
b
|=|
a
-
b
|，则x=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网