题目内容
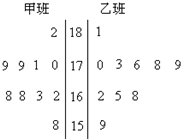 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图(Ⅰ)根据茎叶图判断哪个班的平均身高较高;
(Ⅱ)计算甲班的样本方差
(Ⅲ)现从甲乙两班同学中各选取两名身高不低于170cm的同学,参加四项不同的体育项目,求有多少种不同的安排方法?
考点:茎叶图,极差、方差与标准差
专题:概率与统计
分析:(1)观察茎叶图,可以看出数据的整体水平较高还是较低,有时不用通过具体的数据运算直接看出,有时差别较小,就需要通过数据作出,而本题属于前者.
(2)根据所给的数据,用平均数和方差的公式代入运算,因为数据较多,代入过程中不要出错.
(3)从甲乙两班同学中各选取两名身高不低于170cm的同学的选法有
,然后将四名同学全排的方法有
.
(2)根据所给的数据,用平均数和方差的公式代入运算,因为数据较多,代入过程中不要出错.
(3)从甲乙两班同学中各选取两名身高不低于170cm的同学的选法有
| C | 2 5 |
| C | 2 6 |
| A | 4 4 |
解答:
(1)由茎叶图可知:甲班身高集中于160~179之间,而乙班身高集中于170~180之间.因此乙班平均身高高于甲班;….(3分)
(2)
=
=170
甲班的样本方差为
[(158-170)2+(162-170)2+(163-170)2+(168-170)2+(168-170)2+(170-170)2
+(171-170)2+(179-170)2+(179-170)2]+(182-170)2]=57.(9分)
(3)
=3600…(12分)
(2)
. |
| x |
| 158+162+163+168+168+170+171+179+179+182 |
| 10 |
甲班的样本方差为
| 1 |
| 10 |
+(171-170)2+(179-170)2+(179-170)2]+(182-170)2]=57.(9分)
(3)
| C | 2 5 |
| C | 2 6 |
| A | 4 4 |
点评:求两组数据的平均值和方差是研究数据常做的两件事,平均值反映数据的平均水平,而方差反映数据的波动大小,从两个方面可以准确的把握数据的情况.

练习册系列答案
相关题目
函数f(x)=x2+(2a2-6a)x+2在区间(-∞,2]上单调递减,那么实数a的取值范围( )
| A、[1,+∞) |
| B、(-∞,2] |
| C、[1,2] |
| D、(-∞,1]∪[2,+∞) |
下列函数中,是偶函数且在区间(0,+∞)上是减函数的为( )
A、y=
| ||
| B、y=x2 | ||
C、y=
| ||
D、y=(
|
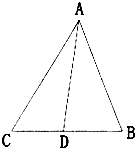 如图,在△ABC中,已知4sin2
如图,在△ABC中,已知4sin2 在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且2b•sinA=
在锐角三角形ABC中,内角A,B,C的对边分别为a,b,c,且2b•sinA=