题目内容
已知△ABC的三边a,b,c成等比数列,且a+c=
,
+
=
.
(Ⅰ)求cosB;
(Ⅱ)求△ABC的面积.
| 21 |
| 1 |
| tanA |
| 1 |
| tanC |
| 5 |
| 4 |
(Ⅰ)求cosB;
(Ⅱ)求△ABC的面积.
考点:正弦定理,余弦定理
专题:解三角形
分析:(Ⅰ)已知等式左边利用同角三角函数间基本关系化简,利用等比数列的性质及正弦定理化简后,求出sinB的值,即可确定出cosB的值;
(Ⅱ)由余弦定理列出关系式,把a+c的值代入求出ac的值,再由sinB的值,利用三角形面积公式即可求出三角形ABC面积.
(Ⅱ)由余弦定理列出关系式,把a+c的值代入求出ac的值,再由sinB的值,利用三角形面积公式即可求出三角形ABC面积.
解答:
解:(Ⅰ)由
+
=
+
=
=
①,
又∵a,b,c成等比数列,∴b2=ac,
由正弦定理化简得:sin2B=sinAsinC,
∵在△ABC中有sin(A+C)=sinB,
∴代入①式得:
=
,即sinB=
,
由b2=ac知,b不是最大边,
∴cosB=
=
;
(Ⅱ)由余弦定理b2=a2+c2-2accosB得,ac=a2+c2-2ac•
=(a+c)2-
ac,
∵a+c=
,∴ac=5,
∴S△ABC=
acsinB=2.
| 1 |
| tanA |
| 1 |
| tanC |
| cosA |
| sinA |
| cosC |
| sinC |
| sin(A+C) |
| sinAsinC |
| 5 |
| 4 |
又∵a,b,c成等比数列,∴b2=ac,
由正弦定理化简得:sin2B=sinAsinC,
∵在△ABC中有sin(A+C)=sinB,
∴代入①式得:
| sinB |
| sin2B |
| 5 |
| 4 |
| 4 |
| 5 |
由b2=ac知,b不是最大边,
∴cosB=
| 1-sin2B |
| 3 |
| 5 |
(Ⅱ)由余弦定理b2=a2+c2-2accosB得,ac=a2+c2-2ac•
| 3 |
| 5 |
| 16 |
| 5 |
∵a+c=
| 21 |
∴S△ABC=
| 1 |
| 2 |
点评:此题考查了正弦、余弦定理,三角形面积公式,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
x,y满足约束条件
,若z=y-2ax取得最大值的最优解不唯一,则实数a的值为( )
|
A、
| ||
B、1或-
| ||
| C、2或1 | ||
| D、2或-1 |
设f(x)=x3+log2(x+
),若a,b∈R,且 f(a)+f(b)≥0,则一定有( )
| x2+1 |
| A、a+b≤0 |
| B、a+b<0 |
| C、a+b≥0 |
| D、a+b>0 |
计算机执行如图的程序语句后,输出的结果是( )


| A、1,3 | B、4,1 |
| C、1,1 | D、4,-2 |
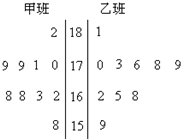 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图