题目内容
下列函数中,是偶函数且在区间(0,+∞)上是减函数的为( )
A、y=
| ||
| B、y=x2 | ||
C、y=
| ||
D、y=(
|
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:本题利用函数的单调性和奇偶性定义判断选项中的函数是否符合条件,得到本题结论.
解答:
解:选项A,
∵f(x)=
,f(-x)=
=-
=-f(x),
∴y=
是奇函数,不合条件;
选项B,
y=x2在(0,+∞)单调递增,不合条件;
选项C,
∵f(x)=
,f(-x)=
=
=f(x),
∴f(x)是偶函数,在区间(0,+∞)上是减函数,符合条件;
选项D,
∵y=(
)x,f(-x)=(
)-x=2x≠(
)x,
∴y=(
)x不是偶函数,不符合条件.
故答案为:C.
∵f(x)=
| 1 |
| x |
| 1 |
| -x |
| 1 |
| x |
∴y=
| 1 |
| x |
选项B,
y=x2在(0,+∞)单调递增,不合条件;
选项C,
∵f(x)=
| 1 |
| x2 |
| 1 |
| (-x)2 |
| 1 |
| x2 |
∴f(x)是偶函数,在区间(0,+∞)上是减函数,符合条件;
选项D,
∵y=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴y=(
| 1 |
| 2 |
故答案为:C.
点评:本题考查了函数的奇偶性和函数的单调性,本题难度不大,属于基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
设f(x)=x3+log2(x+
),若a,b∈R,且 f(a)+f(b)≥0,则一定有( )
| x2+1 |
| A、a+b≤0 |
| B、a+b<0 |
| C、a+b≥0 |
| D、a+b>0 |
函数f(x)=
的值域是( )
| 4-x2 |
| A、(0,2] |
| B、[0,2) |
| C、[0,2] |
| D、(-∞,2] |
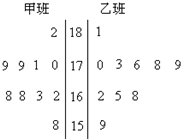 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图