题目内容
12.不等式组$\left\{\begin{array}{l}{x+2y≥0}\\{x-3y≥0}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$表示的平面区域的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{3}{2}$π | C. | π | D. | 3π |
分析 作出不等式组对应的平面区域,结合相应的面积公式即可得到结论.
解答 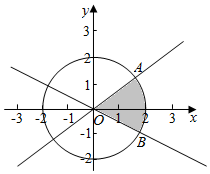 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
OA的斜率k=$\frac{1}{3}$,OB的斜率k=-$\frac{1}{2}$,
则tan∠AOB=$\frac{\frac{1}{3}-(-\frac{1}{2})}{1+\frac{1}{3}•(-\frac{1}{2})}$=1,
则D是圆心角为$\frac{π}{4}$,半径为2的扇形,
故面积为:$\frac{1}{8}$π•4=$\frac{π}{2}$,
故选:A.
点评 本题主要考查平面区域的应用,以及扇形的面积公式,利用数形结合是解决本题的关键,比较基础.

练习册系列答案
相关题目
2.命题p:关于x的不等式(x-2)$\sqrt{{x}^{2}-3x+2}$≥0的解集为{x|x≥2},命题q:若函数y=kx2-kx-1的值恒小于0,则-4<k≤0,那么不正确的是( )
| A. | “非p”为假命题 | B. | “非q”为假命题 | C. | “p或q”为真命题 | D. | “p且q”为假命题 |
7.A={x|x>0},B={x|x2-1<0},A∩B=( )
| A. | {x|-1<x<1} | B. | {x|x>1} | C. | {x|x>0} | D. | {x|0<x<1} |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点左、右分别为F1、F2,点P是双曲线上一点,且$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,P到原点的距离为2,则△PF1F2的面积的取值范围是( )
| A. | (0,2) | B. | (1,2) | C. | (2,4) | D. | (0,4) |
4.在平行四边形ABCD中,AB=2,BC=1,∠ABC=120°,平面ABCD内有一点P,满足AP=$\sqrt{5}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$(λ,μ∈R),则2λ+μ的最大值为( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{15}}{3}$ | C. | $\frac{3\sqrt{5}}{4}$ | D. | $\frac{\sqrt{15}}{6}$ |
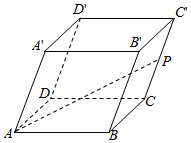 在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.
在平行六面体ABCD-A′B′C′D′中,AB=4,AD=6,AA′=8,∠BAD=90°,∠BAA′=∠DAA′=60°,P是CC1的中点.